HPC Platforms
The term of high performance computing (HPC) implies the use of computing platforms with parallelism beyond what is typical on a laptop or a desktop. On HPC platforms, high performance comes from parallelism that is much larger than that of individual desktop computers and, more fundamentally, parallelim that is taking place on many levels at the same time, as opposed to simply the availability of more processing cores.
As computing hardware becomes more powerful by day, we should note that even on standalone machines of today, HPC practices are oftentimes just as useful as on their supersized counterparts.
HPC hardware would normally include many (multi-core) nodes connected through high speed interconnect, augmented by accelerators (e.g. GPUs), and supported by high-performance networked file systems. For a few examples, let us look at the spec of a few possible configurations:
- Jaguar - a distributed-memory supercomputer. URI: http://www.nccs.gov/computing-resources/jaguar/
- Nautilus - a shared-memory data analysis computer. URI: http://rdav.nics.tennessee.edu/nautilus
- UTK/EECS clusters - typical institutional clusters. URI: http://www.eecs.utk.edu/itdocs/labs/main
FLOPS is a primary metric of HPC performance, but probably one of the least useful for measuring performance of scientific data analysis tasks. One must consider the end to end time that is required to obtain a result. This should include time spent on data movement, I/O overhead for input, data transformation, preprocessing, visualization and I/O overhead for output.
Terminology
Types of Parallelism
Parallel programming is a complex subject, and there are many good and mature technical methods for doing so. Regardless of how you choose the programming tool or model, there is a common way to categorize the overall approach:
- data partition (and implicitly partitioning work), or
- work partition (this time explicitly partitioning work)
The partitions are then assigned to different processing units for concurrent execution, and the goal is that the total execution time gets reduced accordingly. The difficulty is to balance the workload on all of the processing units, and consequently to achieve high parallel scalability (i.e. high parallel utilization).
Weak Scaling and Strong Scaling
There are two performance properties at concern here. (i) When my problem continues to increase in size, it would be great if I can still solve the problem within the same amount of time by simply dedicating proportionally more resources at it. This then means my code has great weak scaling performance. (ii) When my problem stays at the same size, if I can solve the problem 10 times faster by dedicating 10 times more resources, then my code has very good strong scaling performance. Unless you truely measure for these performance numbers, it would be very hard and unrealistic to take estimates, since too many factors are simultaneously at play. We should also note that perfect scalability is nontrivial to achieve, regardless in the form of weak scaling or strong scaling.
It is very common to evaluate scalability through 2D plots, where the horizontal axis is by increasing number of processes (i.e. processing cores) and the vertical axis is some measure of performance. Typical examples for vertical axis would include: speedup factors (e.g. 1000x), system throughput (e.g. 10,000 species per second), measured bandwidth (e.g. 1 gigabytes per second), or total processing time in seconds. These plots also normally assume that some particular factor is held constant, such as constant problem size or constant amount of work dedicated to each processes. It is this implicit factor that determines whether the plot is about weak or strong scaling. The plots of both kinds actually look quite similar in all normal cases. The following are some example scaling curves.
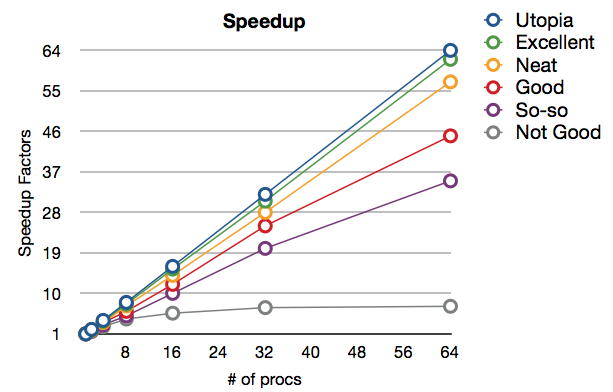
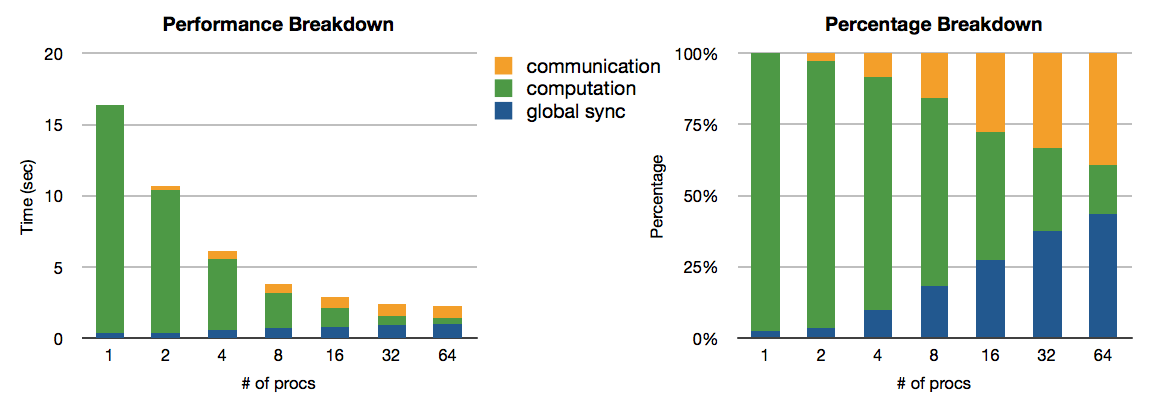
Here we are looking at a strong scaling plot. "Utopia" is the perfect case, where 100% parallel utilization is always achieved. The data collected are for processor counts of 1, 2, 4, 8, 16, 32 and 64. "Not Good" is a bad case where virtually no speedup is obtained after 32 processors have been used. Normal cases are in-between the perfect case and the bad case. As with all computing tasks, taking a closer look means to take more timing results at a finer granularity. So with the "Not Good" case, the following are some performance breakdown results. It is very obvious where the problem is.
HPC Strategies
Good peformance and scalability determine how well we can get a solutions faster and solve a problem that is larger. So that brings the question of how to do it. To answer that, one has to first be lucky to have a problem that would lend itself to scalable parallelization, and also be skillful to develop a correct and efficient implementation of that parallelization method.
Let me first emphasize the "lucky" part. It is actually not just pure luck, because oftentimes there are many ways to pose the problem and potentially many potential solutions. All solutions are not created equal when it comes to parallelization.
Furthermore, being "lucky" is not fully a matter of choosing the right programming tool. It is not necessarily true that one has to use MPI and program in C or Fortran to get performance. So it is quite okay if your analysis tool happens to be written in Java and depends on Java threads for some parallelism.
Besides posing a problem that would fit with HPC environments, there are other specific things to do, such as to (i) increase data locality, (ii) reduce dependencies and (iii) amortize system overheads. But before going over those in detail, I would like to show you a very simple case study.
A Case Study
/* test1 */
#include < stdio.h >
#include < time.h >
#define N 2048
float x[N], y[N], A[N][N];
int main(void)
{
int i,j,irepeat;
float total;
clock_t c1, c2;
c1 = clock();
for (irepeat = 0; irepeat < 5; irepeat ++)
{
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
y[i] = y[i] + A[i][j]*x[j];
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
x[i] = x[i] + A[i][j]*y[j];
}
c2 = clock();
total = (c2 - c1)*1000.f/CLOCKS_PER_SEC;
printf("total time = %6.2f milliseconds\n",
total);
return 0;
}
UNIX> gcc -o test1 test1.c
UNIX> test1
total time taken = 295.19 milliseconds
|
/* test2 */
#include < stdio.h >
#include < time.h >
#define N 2048
float x[N], y[N], A[N][N];
int main(void)
{
int i,j,irepeat;
float total;
clock_t c1, c2;
c1 = clock();
for (irepeat = 0; irepeat < 5; irepeat ++)
{
for (j = 0; j < N; j++)
for (i = 0; i < N; i++)
y[i] = y[i] + A[i][j]*x[j];
for (j = 0; j < N; j++)
for (i = 0; i < N; i++)
x[i] = x[i] + A[i][j]*y[j];
}
c2 = clock();
total = (c2 - c1)*1000.f/CLOCKS_PER_SEC;
printf("total time = %6.2f milliseconds\n",
total);
return 0;
}
UNIX> gcc -o test2 test2.c
UNIX> test2
total time taken = 1779.53 milliseconds
|
Key Concepts
Address Space and Locality
Data together with the "program" itself are stored in a linear space, byte after byte. Multi-dimensional array exists on a conceptual level, with the exact underlying linear storage pattern abstracted away. Although functionally speaking, the storage pattern makes no difference to the program's execution, it is fundamentally important in determining eventual performances.

Due to hierarchical organization of memory (in particular, different levels of cache), data locality is critical for obtaining performance. Using a current 8-core processor as an example: 64KB L1 cache per core, 256KB L2 cache per core, and 24 MB L3 cache shared by all cores. In contrast, the size of the logical address space on a 32-bit architecture is already at 2GB, let alone on 64-bit architectures. The difference between cache size and the actual data size is staggering.
If all of the data would fit into L1 cache, fabulous. If not, then the next best thing is to have as much of the data needed in near future stored in L1 cache, and more data needed futher into future stored in L2 cache, and so on. For general data analysis and visualization users, it is not often that one can have control at this level of granularity because you usually have to depend on some programming tools that offer a higher abstraction level. In this case to achieve data locality, your best bet is to enforce as small a memory footprint as possible (e.g. small partitions of data) for each of your software module.
The next suggestion is to access data efficiently and ideally according to how data is stored. That means, for local data, to use native methods provided by your parallel progrmaming tool as much as possible. For remote data (data stored on a distributed node), consider ways to reduce the need to move data between nodes.
Dependencies and Communication
Pipeline Parallelism underlies everyday use of computer but does not receive the due attention. It is very effective and should be probably be considered as the first thing to try, when you need to accelerate data analysis. Let's take a look at the following example, which is quite common on any platforms of Unix flavors.
UNIX> cat yourscalar_array | extract_contour | gzip -c > contour_data.Z
In this example, "cat" is a program that reads the disk file, "yourscalar_array", and sends its content to "extract_contour" through a pipe. "extract_contour" is a visualization program that extracts a contour from the scalar function as a certain form of geometry. The geometry is then sent on to a 3rd program "gzip" which takes the geometry data as input, compresses the data and writes the compressed data to disk. By doing so, we gain three benefits:
- It is obvious that we have 3 processes running together, and we should expect a speedup by keeping 3 cores busy.
- We also keep multiple devices busy at the same time, which will help to overlap computation and the wait for services done by system devices - another big win in gain performance. essentially rely on magic performed by operating system's scheduler.
- What is less often mentioned is by implementing the tool in this manner, we achieved "streaming" which has the best kind of data locality.
In general data analysis applications, it is getting very common to use different tools for different purposes/tasks. It is the scientist's job to glue the tools together into a complete application. When doing so, please first consider the possibility of using pipeline parallelism. For making the "glue", commonly people use scripting languages such as python, shell and sometimes even C (e.g. fork/exec or system()) or MPI, for performance, security or scalability reasons.
Data Parallelism is also not complicated, but also very very useful in the domain of HPC. These are the cases where data partition is sufficient for managing a parallel run, i.e. data is partitioned and the processing of each data partition is the same on every piece of the data, but totally independent of each other. Applications that fit with data parallelism are sometimes also called "embarrassingly parallel".
For general data analysis, data parallelism means that the scientist can simply cut the input data into partitions of either varying or uniform sizes, and then feed each partition into different instances of the same processing software.
While this model is simple, two technical issues must be taken care of: (1) the workload on each partition may not be equal, and (2) what if you have more data partitions than you have processors. This requires a dynamic job manager/scheduler. For these task, RDAV center has developed an in-house tool called Eden to manage data parallelism jobs. This afternoon you will first hear about a species distribution modeling project that is data paralllel and then see how Eden is used to accelerate modeling runs beyond previously feasible using other systems.
Task Parallelism: many other data analysis applications, however, have innate interdependencies that are hard to avoid because (intermediate) data need to be concurrently shared among execution threads. These are much more complex than pipeline and data paralllel applications. However, I would like to first argue that many problems can be framed differently and many times the change can make a problem fit with pipeline and data parallelism. If your application is indeed task parallel, fine grained programming models are then necessary.
Programming Models
Threading (pthread, java threads, winthread, parallel R, etc.) assumes the model where all of the threads shared the same address space.
Message Passing Interface (MPI: mpich, openMPI, etc.) assumes that none of the processes share the address space, and due to this assumption is the most general and has the best potential for scaling up to larger sized machines.
Threading was designed for shared memory computers, which historically are of smaller scale and form factor (e.g. 4 to 8 processors on an SMP machine). MPI was intended for distributed memory architectures that include 100s to 100,000s of processors. Modern system software and hardware can now make distributed memory machine to also appear as shared memory (i.e. distributed shared memory). RDAV's Nautilus machine is one such example. As evidence of the distributed shared memory capability, we have successfully run pthread based parallel code for ecological data analysis at 512 cores and obtained excellent parallel scalability. But one must still note the performance difference in accessing local vs. remote memory. Later today, you will hear about this subject too, especially in the discussion of "dplace". Tomorrow, you will hear about parallel programming in R on Nautilus.
Lastly, I would like to emphasize again, even when progrmaming using these parallel programming models, the primary design goal is still to increase locality and reduce data sharing and hence the need of communication (either implicit or explicity communication).