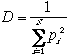
Introduction: A diversity index is a mathematical measure of species diversity in a community. Diversity indices provide more information about community composition than simply species richness (i.e., the number of species present); they also take the relative abundances of different species into account. Consider two communities of 100 individuals each and composed of 10 different species. One community has 10 individuals of each species; the other has one individual of each of nine species, and 91 individuals of the tenth species. Which community is more diverse? Clearly the first one is, but both communities have the same species richness. By taking relative abundances into account, a diversity index depends not only on species richness but also on the evenness, or equitability, with which individuals are distributed among the different species.
Importance: Diversity indices provide important information about rarity and commonness of species in a community. The ability to quantify diversity in this way is an important tool for biologists trying to understand community structure.
Question: How do we measure diversity?
Variables:
| D | Simpson's diversity index |
| S | total number of species in the community (richness) |
| pi | proportion of S made up of the ith species |
| ED | equitability (evenness) |
Methods: Simpson's diversity index (D) is a simple mathematical measure that characterizes species diversity in a community. The proportion of species i relative to the total number of species (pi) is calculated and squared. The squared proportions for all the species are summed, and the reciprocal is taken:
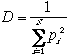
For a given richness (S), D increases as equitability increases, and for a given equitability D increases as richness increases. Equitability (ED) can be calculated by taking Simpson's index (D) and expressing it as a proportion of the maximum value D could assume if individuals in the community were completely evenly distributed (Dmax, which equals S-- as in a case where there was one individual per species). Equitability takes a value between 0 and 1, with 1 being complete evenness.
Siemann et al. (1997) collected the following data on oak savanna arthropod communities to investigate the effects of prescribed burning on arthropods. The abundance data below represent the number of individuals per family (rather than per species) collected in sweep-net sampling during a two year period (1992-1993) (from Siemann et al. 1997).
|
|
|
|
|
|
|
| Araneida | Araneidae |
114
|
0.013
|
33
|
0.024
|
| Misc (5 families) |
66
|
0.008
|
0
|
0.000
|
|
| Coleoptera | Carabidae |
0
|
0.000
|
1
|
0.001
|
| Chrysomelidae |
128
|
0.015
|
58
|
0.042
|
|
| Helodidae |
164
|
0.019
|
5
|
0.004
|
|
| Scarabaeidae |
1
|
0.000
|
2
|
0.001
|
|
| Staphylinidae |
5
|
0.001
|
2
|
0.001
|
|
| Misc (23 families) |
477
|
0.056
|
56
|
0.041
|
|
| Diptera | Anthomyiidae |
262
|
0.031
|
172
|
0.125
|
| Chamaemyidae |
27
|
0.003
|
29
|
0.021
|
|
| Chironomidae |
0
|
0.000
|
0
|
0.000
|
|
| Chloropidae |
87
|
0.010
|
1
|
0.001
|
|
| Culicidae |
0
|
0.000
|
6
|
0.004
|
|
| Dolichopodidae |
315
|
0.037
|
117
|
0.085
|
|
| Platystomatidae |
345
|
0.040
|
137
|
0.099
|
|
| Syrphidae |
100
|
0.012
|
29
|
0.021
|
|
| Tephritidae |
191
|
0.022
|
3
|
0.002
|
|
| Misc (26 families) |
438
|
0.051
|
111
|
0.080
|
|
| Hemiptera | Miridae |
2177
|
0.254
|
55
|
0.040
|
| Misc (10 families) |
150
|
0.018
|
29
|
0.021
|
|
| Homoptera | Aphididae |
0
|
0.000
|
0
|
0.000
|
| Cicadellidae |
1465
|
0.171
|
86
|
0.062
|
|
| Delphacidae |
272
|
0.032
|
21
|
0.015
|
|
| Membracidae |
265
|
0.031
|
23
|
0.017
|
|
| Misc (6 families) |
132
|
0.015
|
4
|
0.003
|
|
| Hymenoptera | Formicidae |
0
|
0.000
|
0
|
0.000
|
| Misc (28 families) |
316
|
0.037
|
24
|
0.017
|
|
| Lepidoptera | Noctuidae |
72
|
0.008
|
5
|
0.004
|
| Pyralidae |
13
|
0.002
|
20
|
0.015
|
|
| Tortricidae |
8
|
0.001
|
0
|
0.000
|
|
| Misc (4 families) |
73
|
0.009
|
0
|
0.000
|
|
| Odonata | Coenagrionidae |
0
|
0.000
|
202
|
0.146
|
| Misc (2 families) |
0
|
0.000
|
2
|
0.001
|
|
| Orthoptera | Acrididae |
564
|
0.066
|
138
|
0.100
|
| Gryllidae |
4
|
0.000
|
0
|
0.000
|
|
| Tettigoniidae |
264
|
0.031
|
0
|
0.000
|
|
| Misc (3 families) |
3
|
0.000
|
0
|
0.000
|
|
| Trichoptera | Leptoceridae |
0
|
0.000
|
0
|
0.000
|
| Phryganeidae |
0
|
0.000
|
0
|
0.000
|
|
| Miscellaneous | (3 orders, 4 families) |
63
|
0.007
|
8
|
0.006
|
Although we do not have species data, we can calculate family diversity and equitability using these data. The proportions (pi values) have been calculated by dividing the number of individuals in a given family by the total number of individuals collected in a year (8,561 in 1992 and 1,379 in 1993). To calculate Simpson's D, we square each proportion (pi), sum these squared values, and take the reciprocal (divide one by the sum). For example, for the 1992 data, Simpson's D is calculated (1 / [0.0132 + 0.0082 + 0.0002 + 0.0152 + ... + 0.0072]) = 8.732. We could then calculate the equitability (ED) quite easily using the second equation above (ED = D / Dmax, with Dmax = S). Here, we will use the number of families in place of S, so that E = 8.732 / 31 = 0.2817.
Interpretation: What we have calculated is an index of family diversity and evenness, rather than the standard index of species diversity and evenness. Based on the value of 0.2817 calculated for ED, we could describe the equitability, or evenness of individuals' distributions among families, in this community as relatively low (recall that ED assumes a value between 0 and 1, and 1 is complete equitability).
Conclusions: Simpson's D is one of many diversity indices used by biologists. Others include the Shannon index (H), the Berger-Parker index (d), Hill's N1, and Q-statistics. Each of these indices has strengths and weaknesses. An ideal index would discriminate clearly and accurately between samples, not be greatly affected by differences in sample size, and be relatively simple to calculate. Biologists often use a combination of several indices to take advantages of the strengths of each and develop a more complete understanding of community structure.
Additional Question:
1. Calculate D and ED for the 1993 samples. How do these values compare to the ones calculated for the 1992 samples?
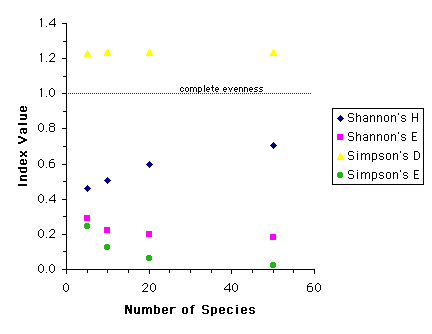
2. The following graph shows two different diversity indices (Simpson's D and Shannon's Hand their associated evenness indices (ED and EH) calculated for four communities composed of 5, 10, 20 and 50 species, respectively. In each community, 90% of the individuals belong to one species, and the other 10% of the individuals are evenly divided among the remaining species. How do the indices differ across communities? (The diversity indices, and therefore the evenness indices, cannot be compared directly to one another, but we can compare how they change for the different communities). Would your conclusions about these communities be different depending on which diversity index you used?
Sources: Begon, M., J. L. Harper, and C. R. Townsend. 1996. Ecology: Individuals, Populations, and Communities, 3rd edition. Blackwell Science Ltd., Cambridge, MA.
Magurran, A. E. 1988. Ecological Diversity and its Measurement. Princeton University Press, Princeton, NJ.
Rosenzweig, M. L. 1995. Species Diversity in Space and Time. Cambridge University Press, New York, NY.
Siemann, E., J. Haarstad, and D. Tilman. 1997. Short-term and long-term effects of burning on oak savanna arthropods. American Midland Naturalist 137:349-361.
copyright 1999 M. Beals, L. Gross, S. Harrell