ESTIMATION OF TREE HEIGHT: RIGHT TRIANGLE TRIGONOMETRY

Introduction:  Scientists studying a forest ecosystem over a long period of time may record measurements of trees for a number of variables, including each tree's diameter at breast height, height of the lowest living branch, canopy cover, etc. One aspect of a tree's growth that can be hard to measure is tree height. Forest researchers sometimes use a piece of equipment consisting of telescoping components, which are extended until the tip reaches the same height as the tree top (this requires a second researcher standing at a distance from the tree to determine when the tip is at the correct height). This method can be cumbersome, as the equipment is bulky and the measurements require two people.

Importance:  The measurement of tree growth in a forest over time provides important information about the dynamics of that ecosystem. Growth rates can reflect, among other things, differing availability of water, carbohydrates, or nutrients in different sites or from season to season or year to year.

Question:  Is there an efficient way to measure tree height, without heavy equipment and multiple people?

Variables:
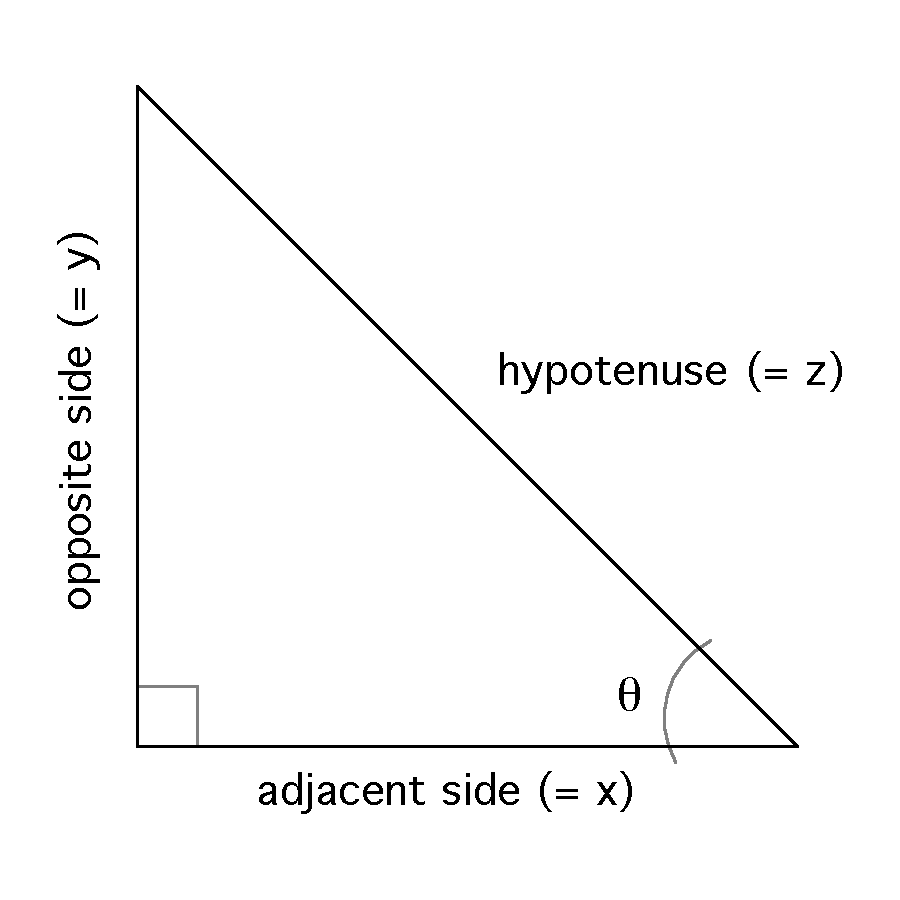
q an acute angle of a right triangle
x side of a triangle adjacent to the angle q
y side of a triangle opposite the angle q
z the hypotenuse of a triangle

Methods:  Trigonometry is a branch of mathematics dealing with measurements of the angles and sides of triangles, and functions based on these measurements. The three basic trigonometric functions that we are concerned with here (sine, cosine, and tangent) are ratios of the lengths of two sides of a triangle. These ratios are the trigonometric functions of an angle, theta, such that
 
 



where q (theta) is the angle of interest, "opp" is the length of the side of the triangle opposite q (y), "hyp" is the length of the hypotenuse (z), and "adj" is the length of the side adjacent to the angle q (x), as illustrated on the triangle below.

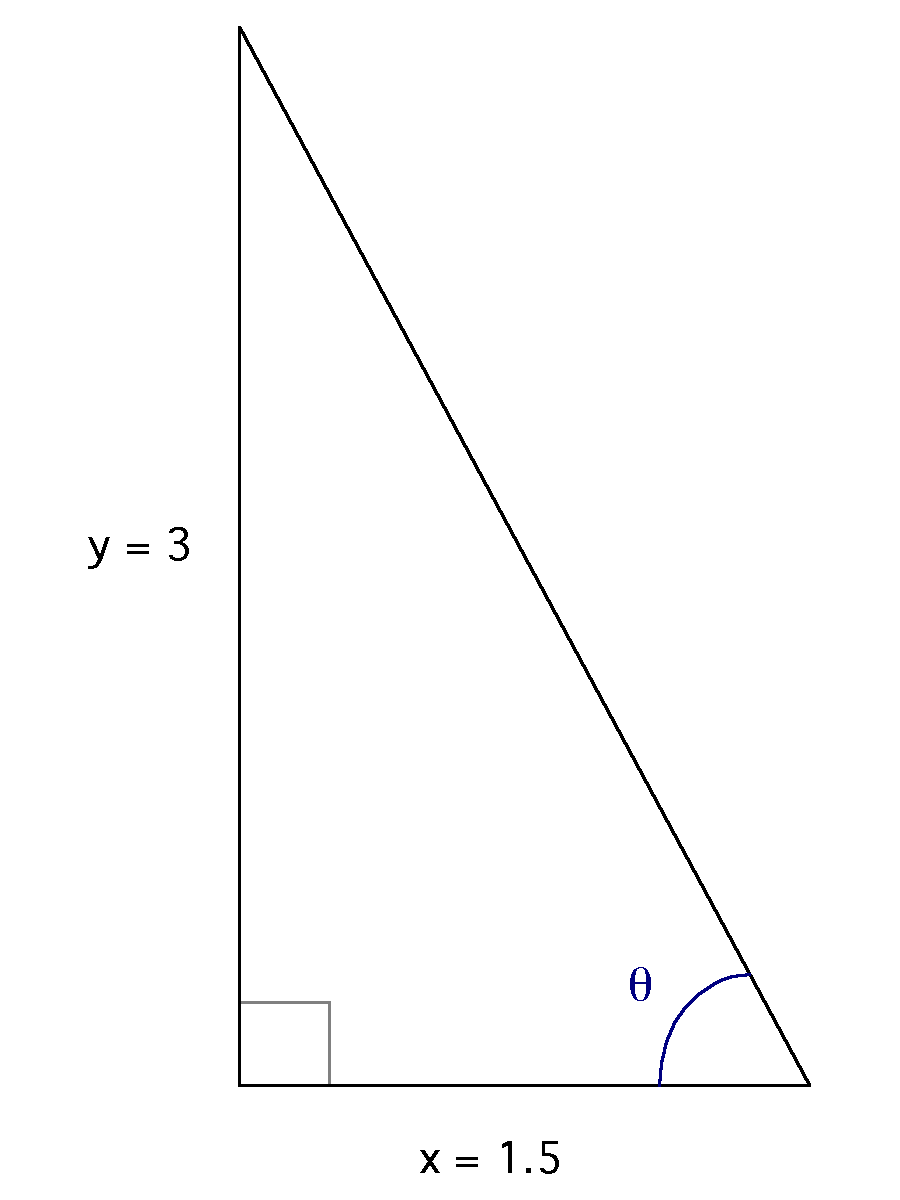
If we know the lengths of two sides of a right triangle (recall from geometry that a right triangle has one angle that is 90 degrees [a right angle]), we can calculate the length of the third side using the Pythagorean theorem (opp2 + adj2 = hyp2, or y2 + x2 = z2). For the triangle below, the side opposite q is three units in length, and the side adjacent to q is 1.5 units in length.

The length of the hypotenuse is calculated 32 + 1.52 = hyp2 =11.25. Taking the square root of 11.25, we find that the hypotenuse is approximately 3.35 units long. We now know the lengths of each of the sides of the triangle, and can use these to find values for the trigonometric functions:
 
 



But what can we do with this information? Well, for one thing we can use it to find q by taking the inverse of any of the functions (for our purposes here can do this using a calculator). Doing this we see that q is an angle of approximately 63.4 degrees.

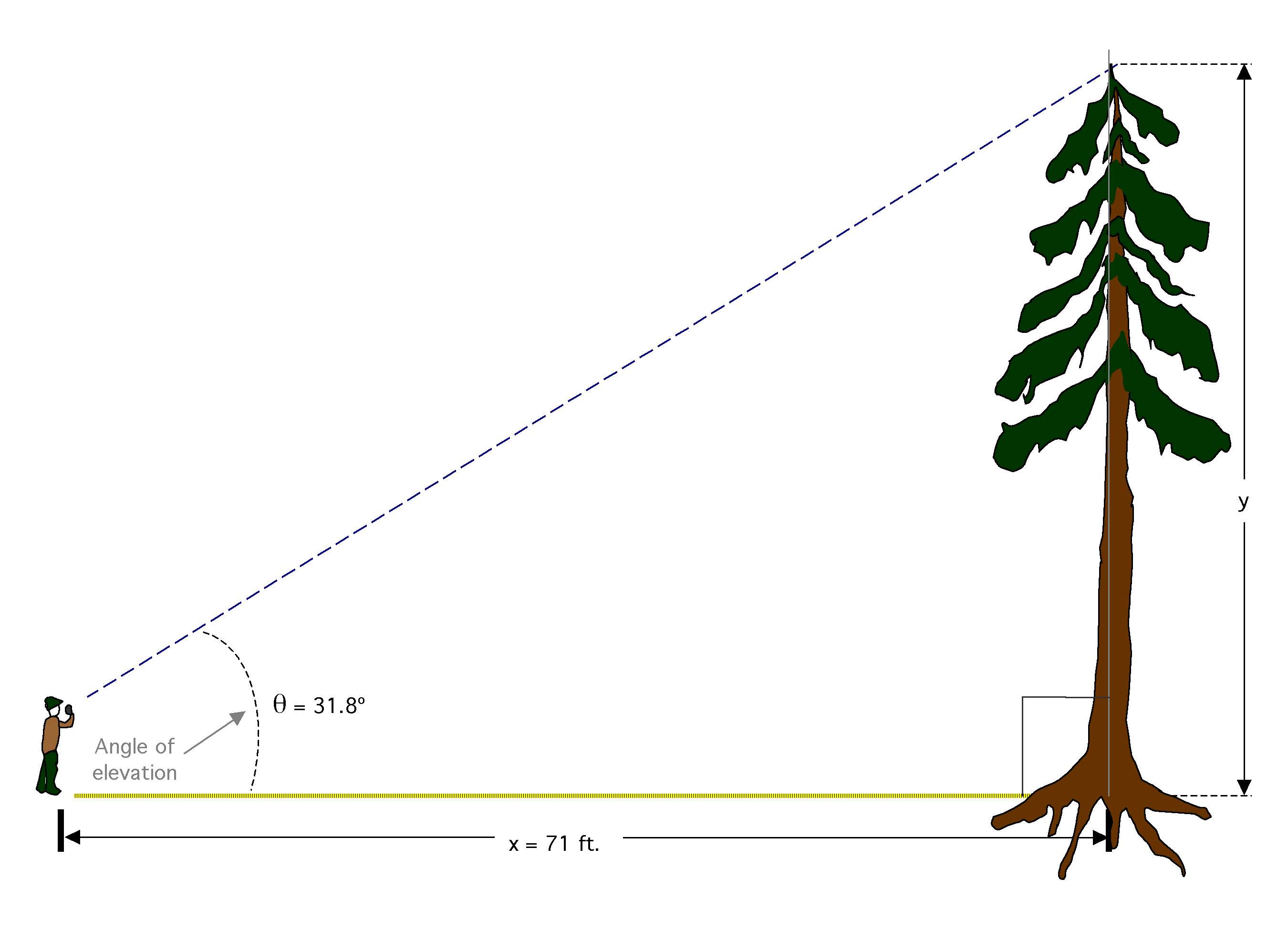
The drawing below shows a forester measuring a tree's height using trigonometry. Assuming that the tree is at a right angle to the plane on which the forester is standing, the base of the tree, the top of the tree, and the forester form the vertices (or corners) of a right triangle. The forester measures his or her distance from the base of the tree, and then uses a clinometer (a small instrument that measures inclination, or angle of elevation) to look at the top of the tree and determine q .

Interpretation: In this situation, rather than knowing the lengths of all of the sides, we know q and the length of the adjacent side (x), and are interested in determining the length of the opposite side (y, the height of the tree). Which of the three trigonometric functions deals with the adjacent and opposite sides?
 
 



We know q , and we know "adj" (or x); multiplying both sides of the equation by "adj" or x and substituting our known values, we get
 
 



The tree is approximately 44 feet tall.

Conclusions: Trigonometry has many real-world applications. In the example here, it can be used so that forest researchers don't have to carry around additional equipment and are able to collect the necessary information for calculating tree heights quickly and efficiently in the field.

Additional Questions:
1) You know from your geometry class that all the angles of a triangle must sum to 180 degrees. Therefore, the third angle from the tree and forester triangle must be (180 degrees - 90 degrees - 31.8 degrees) = 58.2 degrees. Verify this using the three trigonometric functions (note that for this angle, y is the adjacent side and x is the opposite side).

2) What would the angle of elevation (q ) be if the tree was 100 ft. tall?

Sources:
Larson, R. E., R. P. Hostetler, and B. H. Edwards. 1993. Precalculus: A Graphing Approach. D. C. Heath and Company, Lexington, MA.

Waring, R. H. and W. H. Schlesinger. 1985. Forest Ecosystems: Concepts and Management. Academic Press, Inc. San Diego, CA.

copyright 2000  M. Beals, L. Gross, S. Harrell