Introduction to Matrices and Modeling in Biology
A central theme in biology is that biological objects of
interest have structure that may affect the way those objects should be
analyzed. Moving up the hierarchical biological scale, examples include the various
components of cells, the cellular composition of tissues, the tissue
composition of individual organisms, the composition of different individuals
which make up a population, the species which make up a community and the types
of habitat across a landscape. Each of these biological entities has a
sub-structure. Think of different types of individuals within a population: the
males and females of different ages in a meerkat population, the demographic
(age, location, economic status, etc.) structure of a human population, the
chemical composition of cells, etc. One of the most useful mathematical
concepts provides a way to describe the composition of these biological
objects, and provides a mechanism to analyze how the composition might change
through time or across space.
A motivating example that we will use regularly in this
section of the course concerns patterns of species across a landscape. Think of
taking aerial photographs of a plot of land once each decade, following the
changes in pattern across the landscape. On a real landscape, this could be
looking at species, communities of plants (deciduous hardwoods, herbacious,
grassland, etc.), or land-use (agricultural, urban, suburban, etc.). For each
decade you have an photo in which you might be able to classify each area as
consisting of one of a few species. Then one descriptive summary you might use
for the landscape is to describe it by the fraction of the total area which is
covered by each of the species. In the EcoBeaker example, this corresponds to
what fraction of the landscape pictured on the computer is of the different
colors, representing different types of organisms (grass, blackberry bushes,
hickory trees, etc.).
Describing this landscape at a particular time then could
use a list of numbers giving the fraction of the landscape of each species, in
other words a vector of numbers which sum to one. Pictorially, this description
corresponds to the bar charts illustrated in the EcoBeaker example, showing the
number of squares in each landscape covered by each type of organism. There is
of course a loss of information in going from the picture of the landscape to a
simple list of numbers representing the fraction of the landscape of each type.
All information about the spatial arrangement is lost - that is we can't tell
from just a vector of numbers whether all the grass is clustered on one side of
the landscape or whether it is dispersed throughout the landscape.
As time goes on (e.g. we take a picture of the landscape
every decade), the vector describing the fraction covered by each type of
organism will change. If we could determine the rules by which this vector
changes, we would have a basis for a model of the landscape's dynamics (called
succession in ecology). From this model we might then be able to determine from
just a few decades of pictures, what the landscape might look like many decades
from now (the process we called extrapolation when we were talking about
regressions).
Note that this entire area of looking at landscapes and
how they can be described and how they change is part of the field of
geography. The main tool used to analyze changes is called Geographical
Information Systems (GIS), which is a fancy name for software that allows you
to look at, build and manipulate maps.
Our objective in this section of the course is to
construct the mathematical tools needed to analyze changes in vectors
describing landscapes. This doesn't just apply to landscapes though. It applies
to any biological entity which can be broken down into discrete classes. So we
will be able to use this to describe changes in the age breakdown of human
population of Knoxville (or any other region). This is the basis for the entire
field of demography - the study of changes in the structure of human populations
through time and space. But this is just as easily applied to any population -
bears in the Smokies, killer whales in the Pacific, meerkats in South Africa,
etc. More than that however, it applies to an immense number of biological
problems from cell population dynamics (think of bacterial populations in which
you follow which bacteria are resistant to each of a list of antibiotics), to
behavior (think of the fraction of a group of meerkats carrying out each of a
list of behaviors), to pharmacokinetics (think of the fraction of a drug
infused into the body in each of a list of tissues and how this changes through
time - there would be a class here called "removed" in which the drug
has been excreted).
It turns out that the mathematics which allows us to
describe changes in the structure of biological entities or landscapes is
simply described by building an appropriate set of rules for manipulating
numbers that are arranged in particular orders. The order matters because the
way we describe these structures depends upon the order that you list the
numbers. So a vector that describes the fraction of the landscape in (grass,
shrub, trees) as (.2, .5, .3) is different from the vector (.5, .2, .3) - these
represent very different landscapes - the order of the numbers matters. So we
have to build up a way of manipulating numbers in which order matters - this is
different from the typical rules of algebra you have seen since middle school.
We essentially have to come up with a way to manipulate vectors in the same way
you used the algebraic manipulations (addition, subtraction, multiplication and
division) for single numbers (single numbers are called "scalars" to
differentiate them from vectors which consist of lists of numbers in particular
orders). Just as numbers can be represented in general by a letter (the
essential idea of algebra you've seen since high school), vectors can be
represented by letters, and the elements of a vector (the numbers which make it
up) can be letters (algebraic entities) as well.
So what is a "Matrix" - yes it is the movie,
but in our case it simply represents a list of numbers arranged in a
2-dimensional array:
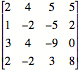
Yes this is just like the cascading stream of numbers in
the movie, but in this case they are not cascading - just static. What we will
do in this section of the course is first describe an algebra for how to do the
basic algebraic manipulations of vectors (just a row or column of numbers
arranged in a particular order) and matrices (the plural of matrix) which are
rectangular arrays of numbers.
Our objective in describing this area of mathematics
(called Matrix Algebra or Linear Algebra) is to get to the point of being able
to describe mathematically how the structure of a landscape, population, etc.
changes through time.
One way to express this is similar to the notion that had
for the equation describing exponential growth of a population - N(t)= N(0)
exp(-kt). Only this just describes how a single number giving the entire
population size of density (numbers of individuals per unit area or per unit
volume) changes with time. When we want to describe how a population with
structure changes, we need to express how a vector changes with time. If this
is in discrete periods, say from one year to the next, then we might express
how we go from a vector of population structure at time t, N(t) to a vector of population structure at time t+1,
N(t+1). (Note that I am using Bold
Type here to indicate that we are dealing
with a vector or matrix, not a scalar). To be able to do this, we need to learn
some basics of matrix manipulations.
Matrix algebra - basic operations
These are described in Section 55 of the text. This
includes the definition of an m x n matrix (m rows and n columns), what it
means to say that two matrices are equal (the element in a row and column of
one matrix is the same as the element in the same row and column of the second
matrix, and this holds for all elements), how to add matrices (you can only do
this if they are the same size and then you add each element of the first
matrix to the corresponding element of the second matrix to get the sum), how
to subtract matrices (the same as addition, only you subtract element by
element), how to multiply (can only do this if the number of columns of the
first matrix is the same as the number of rows of the second matrix), and the
basic laws of matrix algebra (the same as standard arithmetic, except that the
commutative law doesn't hold in general, so that A B is not the same as B A for two matrices A and B.