 |
Peter Müller
pmueller@uu-gna.mit.edu
Globewide Network Academy (GNA)
www.gnacademy.org/
September 4, 1997
Then, the ``bomb''. The original author of the used ASCII tutorial stands on his copyright and denies us to reuse his work. Unfortunately, Marcus was unable to spend more time on this project and so the main driving force was gone.
My experiences made as consultant for this first course have lead to my decision that the course must be offered again. So, in Summer 1995 I've just announced a second round, hoping that somehow a new tutorial could be written. Well, here is the result. I hope, that you find this tutorial useful and clear. If not, please send me a note. The tutorial is intended to be a group work and not a work of one person. It is essential, that you express your comments and suggestions.
The course and the tutorial could have only been realized with help of many people. I wish to thank the people from the Globewide Network Academy (GNA), especially Joseph Wang and Susanne Reading.
Ricardo Nassif and David Klein provide me with suggestions to improve the readability of the tutorial.
The complete tutorial is available free of charge in PostScript in
both US letter and DIN A4 paper formats. Please check out
http://www.zib.de/mueller/Course/Tutorial/Postscript/
.
Berlin, Germany
Peter Müller
Some people will say that object-orientation is ``modern''. When reading announcements of new products everything seems to be ``object-oriented''. ``Objects'' are everywhere. In this tutorial we will try to outline characteristics of object-orientation to allow you to judge those object-oriented products.
The tutorial is organized as follows. Chapter 2 presents a brief overview of procedural programming to refresh your knowledge in that area. Abstract data types are introduced in chapter 3 as a fundamental concept of object-orientation. After that we can start to define general terms and beginning to view the world as consisting of objects (chapter 4). Subsequent chapters present fundamental object-oriented concepts (chapters 5 and 6). Chapters 7 through 9 introduce C++ as an example of an object-oriented programming language which is in wide-spread use. Finally chapter 10 demonstrates how to apply object-oriented programming to a real example.
This chapter is a short survey of programming techniques. We use a simple example to illustrate the particular properties and to point out their main ideas and problems.
Roughly speaking, we can distinguish the following learning curve of someone who learns to program:
This chapter is organized as follows. Sections 2.1 to 2.3 briefly describe the first three programming techniques. Subsequently, we present a simple example of how modular programming can be used to implement a singly linked list module (section 2.4). Using this we state a few problems with this kind of technique in section 2.5. Finally, section 2.6 describes the fourth programming technique.
As you should all know, this programming techniques provide tremendous disadvantages once the program gets sufficiently large. For example, if the same statement sequence is needed at different locations within the program, the sequence must be copied. This has lead to the idea to extract these sequences, name them and offering a technique to call and return from these procedures.
 |
With introducing parameters as well as procedures of procedures ( subprocedures) programs can now be written more structured and error free. For example, if a procedure is correct, every time it is used it produces correct results. Consequently, in cases of errors you can narrow your search to those places which are not proven to be correct.
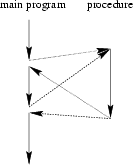
Now a program can be viewed as a sequence of procedure calls![[*]](foot.gif) . The main program is responsible to pass data to the
individual calls, the data is processed by the procedures and, once the
program has finished, the resulting data is presented. Thus, the flow of
data can be illustrated as a hierarchical graph, a tree, as shown in
Fig. 2.3 for a program with no subprocedures.
. The main program is responsible to pass data to the
individual calls, the data is processed by the procedures and, once the
program has finished, the resulting data is presented. Thus, the flow of
data can be illustrated as a hierarchical graph, a tree, as shown in
Fig. 2.3 for a program with no subprocedures.
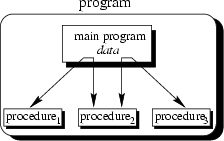 |
To sum up: Now we have a single program which is devided into small pieces called procedures. To enable usage of general procedures or groups of procedures also in other programs, they must be separately available. For that reason, modular programming allows grouping of procedures into modules.
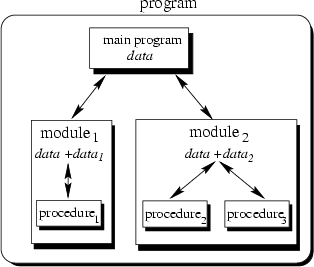 |
Each module can have its own data. This allows each module to manage an internal state which is modified by calls to procedures of this module. However, there is only one state per module and each module exists at most once in the whole program.
Singly linked lists just provides access methods to append a new element to their end and to delete the element at the front. Complex data structures might use already existing ones. For example a queue can be structured like a singly linked list. However, queues provide access methods to put a data element at the end and to get the first data element (first-in first-out (FIFO) behaviour).
We will now present an example which we use to present some design concepts. Since this example is just used to illustrate these concepts and problems it is neither complete nor optimal. Refer to chapter 10 for a complete object-oriented discussion about the design of data structures.
Suppose you want to program a list in a modular programming language such as C or Modula-2. As you believe that lists are a common data structure, you decide to implement it in a separate module. Typically, this requires you to write two files: the interface definition and the implementation file. Within this chapter we will use a very simple pseudo code which you should understand immediately. Let's assume, that comments are enclosed in ``/* ... */''. Our interface definition might then look similar to that below:
/*
* Interface definition for a module which implements
* a singly linked list for storing data of any type.
*/
MODULE Singly-Linked-List-1
BOOL list_initialize();
BOOL list_append(ANY data);
BOOL list_delete();
list_end();
ANY list_getFirst();
ANY list_getNext();
BOOL list_isEmpty();
END Singly-Linked-List-1
Interface definitions just describe what is available and not how it is made available. You hide the information of the implementation in the implementation file. This is a fundamental principle in software engineering, so let's repeat it: You hide information of the actual implementation (information hiding). This enables you to change the implementation, for example to use a faster but more memory consuming algorithm for storing elements without the need to change other modules of your program: The calls to provided procedures remain the same.
The idea of this interface is as follows: Before using the list one has to
call list_initialize() to initialize variables local to the module. The
following two procedures implement the mentioned access methods append
and delete. The append procedure needs a more detailed discussion.
Function list_append() takes one argument data of arbitrary type.
This is necessary since
you wish to use your list in several different environments, hence, the type
of the data elements to be stored in the list is not known beforehand.
Consequently, you have to use a special type ANY which allows to assign
data of any type to it![[*]](foot.gif) .
The third procedure list_end() needs to be
called when the program
terminates to enable the module to clean up its internally used variables. For
example you might want to release allocated memory.
.
The third procedure list_end() needs to be
called when the program
terminates to enable the module to clean up its internally used variables. For
example you might want to release allocated memory.
With the next two procedures list_getFirst() and list_getNext() a simple mechanism to traverse through the list is offered. Traversing can be done using the following loop:
ANY data;
data <- list_getFirst();
WHILE data IS VALID DO
doSomething(data);
data <- list_getNext();
END
Now you have a list module which allows you to use a list with any type of data elements. But what, if you need more than one list in one of your programs?
/*
* A list module for more than one list.
*/
MODULE Singly-Linked-List-2
DECLARE TYPE list_handle_t;
list_handle_t list_create();
list_destroy(list_handle_t this);
BOOL list_append(list_handle_t this, ANY data);
ANY list_getFirst(list_handle_t this);
ANY list_getNext(list_handle_t this);
BOOL list_isEmpty(list_handle_t this);
END Singly-Linked-List-2;
You use DECLARE TYPE to introduce a new type list_handle_t which represents your list handle. We do not specify, how this handle is actually represented or even implemented. You also hide the implementation details of this type in your implementation file. Note the difference to the previous version where you just hide functions or procedures, respectively. Now you also hide information for an user defined data type called list_handle_t.
You use list_create() to obtain a handle to a new thus empty list. Every other procedure now contains the special parameter this which just identifies the list in question. All procedures now operate on this handle rather than a module global list.
Now you might say, that you can create list objects. Each such object can be uniquely identified by its handle and only those methods are applicable which are defined to operate on this handle.
In the example every time you want to use a list, you explicitly have to declare a handle and perform a call to list_create() to obtain a valid one. After the use of the list you must explicitly call list_destroy() with the handle of the list you want to be destroyed. If you want to use a list within a procedure, say, foo() you use the following code frame:
PROCEDURE foo() BEGIN
list_handle_t myList;
myList <- list_create();
/* Do something with myList */
...
list_destroy(myList);
END
Let's compare the list with other data types, for example an integer. Integers are declared within a particular scope (for example within a procedure). Once you've defined them, you can use them. Once you leave the scope (for example the procedure where the integer was defined) the integer is lost. It is automatically created and destroyed. Some compilers even initialize newly created integers to a specific value, typically 0 (zero).
Where is the difference to list ``objects''? The lifetime of a list is also defined by its scope, hence, it must be created once the scope is entered and destroyed once it is left. On creation time a list should be initialized to be empty. Therefore we would like to be able to define a list similar to the definition of an integer. A code frame for this would look like this:
PROCEDURE foo() BEGIN
list_handle_t myList; /* List is created and initialized */
/* Do something with the myList */
...
END /* myList is destroyed */
The advantage is, that now the compiler takes care of calling initialization and termination procedures as appropriate. For example, this ensures that the list is correctly deleted, returning resources to the program.
Decoupling of data and operations leads usually to a structure based on the operations rather than the data: Modules group common operations (such as those list_...() operations) together. You then use these operations by providing explicitly the data to them on which they should operate. The resulting module structure is therefore oriented on the operations rather than the actual data. One could say that the defined operations specify the data to be used.
In object-orientation, structure is organized by the data. You choose the data representations which best fit your requirements. Consequently, your programs get structured by the data rather than operations. Thus, it is exactly the other way around: Data specifies valid operations. Now modules group data representations together.
PROCEDURE foo() BEGIN
SomeDataType data1;
SomeOtherType data2;
list_handle_t myList;
myList <- list_create();
list_append(myList, data1);
list_append(myList, data2); /* Oops */
...
list_destroy(myList);
END
It is in your responsibility to ensure that your list is used consistently. A possible solution is to additionally add information about the type to each list element. However, this implies more overhead and does not prevent you from knowing what you are doing.
What we would like to have is a mechanism which allows us to specify on which data type the list should be defined. The overall function of the list is always the same, whether we store apples, numbers, cars or even lists. Therefore it would be nice to declare a new list with something like:
list_handle_t<Apple> list1; /* a list of apples */
list_handle_t<Car> list2; /* a list of cars */
The corresponding list routines should then automatically return the correct data types. The compiler should be able to check for type consistency.
The list example implies operations to traverse through the list. Typically a cursor is used for that purpose which points to the current element. This implies a traversing strategy which defines the order in which the elements of the data structure are to be visited.
For a simple data structure like the singly linked list one can think of only one traversing strategy. Starting with the leftmost element one successively visits the right neighbours until one reaches the last element. However, more complex data structures such as trees can be traversed using different strategies. Even worse, sometimes traversing strategies depend on the particular context in which a data structure is used. Consequently, it makes sense to separate the actual representation or shape of the data structure from its traversing strategy. We will investigate this in more detail in chapter 10.
What we have shown with the traversing strategy applies to other strategies as well. For example insertion might be done such that an order over the elements is achieved or not.
 |
Consider the multiple lists example again. The problem here with modular programming is, that you must explicitly create and destroy your list handles. Then you use the procedures of the module to modify each of your handles.
In contrast to that, in object-oriented programming we would have as many list objects as needed. Instead of calling a procedure which we must provide with the correct list handle, we would directly send a message to the list object in question. Roughly speaking, each object implements its own module allowing for example many lists to coexist.
Each object is responsible to initialize and destroy itself correctly. Consequently, there is no longer the need to explicitly call a creation or termination procedure.
You might ask: So what? Isn't this just a more fancier modular programming technique? You were right, if this would be all about object-orientation. Fortunately, it is not. Beginning with the next chapters additional features of object-orientation are introduced which makes object-oriented programming to a new programming technique.
Some authors describe object-oriented programming as programming abstract data types and their relationships. Within this section we introduce abstract data types as a basic concept for object-orientation and we explore concepts used in the list example of the last section in more detail.
The first thing with which one is confronted when writing programs is the problem. Typically you are confronted with ``real-life'' problems and you want to make life easier by providing a program for the problem. However, real-life problems are nebulous and the first thing you have to do is to try to understand the problem to separate necessary from unnecessary details: You try to obtain your own abstract view, or model, of the problem. This process of modeling is called abstraction and is illustrated in Figure 3.1.
The model defines an abstract view to the problem. This implies that the model focusses only on problem related stuff and that you try to define properties of the problem. These properties include
by the problem.
As an example consider the administration of employees in an institution. The head of the administration comes to you and ask you to create a program which allows to administer the employees. Well, this is not very specific. For example, what employee information is needed by the administration? What tasks should be allowed? Employees are real persons who can be characterized with many properties; very few are:
Certainly not all of these properties are necessary to solve the administration problem. Only some of them are problem specific. Consequently you create a model of an employee for the problem. This model only implies properties which are needed to fulfill the requirements of the administration, for instance name, date of birth and social number. These properties are called the data of the (employee) model. Now you have described real persons with help of an abstract employee.
Of course, the pure description is not enough. There must be some operations defined with which the administration is able to handle the abstract employees. For example, there must be an operation which allows you to create a new employee once a new person enters the institution. Consequently, you have to identify the operations which should be able to be performed on an abstract employee. You also decide to allow access to the employees' data only with associated operations. This allows you to ensure that data elements are always in a proper state. For example you are able to check if a provided date is valid.
To sum up, abstraction is the structuring of a nebulous problem into well-defined entities by defining their data and operations. Consequently, these entities combine data and operations. They are not decoupled from each other.
The example of the previous section shows, that with abstraction you create a well-defined entity which can be properly handled. These entities define the data structure of a set of items. For example, each administered employee has a name, date of birth and social number.
The data structure can only be accessed with defined operations. This set of operations is called interface and is exported by the entity. An entity with the properties just described is called an abstract data type (ADT).
Figure 3.2 shows an ADT which consists of an abstract data structure and operations. Only the operations are viewable from the outside and define the interface.
Once a new employee is ``created'' the data structure is filled with actual values: You now have an instance of an abstract employee. You can create as many instances of an abstract employee as needed to describe every real employed person.
Let's try to put the characteristics of an ADT in a more formal way:
Definition (Abstract Data Type) An abstract data type (ADT) is
characterized
by the following properties:
With the first property it is possible to create more than one instance of an ADT as exemplified with the employee example. You might also remember the list example of chapter 2. In the first version we have implemented a list as a module and were only able to use one list at a time. The second version introduces the ``handle'' as a reference to a ``list object''. From what we have learned now, the handle in conjunction with the operations defined in the list module defines an ADT List:
However, all of these properties are only valid due to our understanding of and our discipline in using the list module. It is in our responsibility to use instances of List according to these rules.
The principle of hiding the used data structure and to only provide a well-defined interface is known as encapsulation. Why is it so important to encapsulate the data structure?
To answer this question consider the following mathematical example where we want to define an ADT for complex numbers. For the following it is enough to know that complex numbers consists of two parts: real part and imaginary part. Both parts are represented by real numbers. Complex numbers define several operations: addition, substraction, multiplication or division to name a few. Axioms and preconditions are valid as defined by the mathematical definition of complex numbers. For example, it exists a neutral element for addition.
To represent a complex number it is necessary to define the data structure to be used by its ADT. One can think of at least two possibilities to do this:
Point 3 of the ADT definition says that for each access to the data structure there must be an operation defined. The above access examples seem to contradict this requirement. Is this really true?
Let's look again at the two possibilities for representing imaginary numbers. Let's stick to the real part. In the first version, x equals c[0]. In the second version, x equals c.r. In both cases x equals ``something''. It is this ``something'' which differs from the actual data structure used. But in both cases the performed operation ``equal'' has the same meaning to declare x to be equal to the real part of the complex number c: both cases archieve the same semantics.
If you think of more complex operations the impact of decoupling data structures from operations becomes even more clear. For example the addition of two complex numbers requires you to perform an addition for each part. Consequently, you must access the value of each part which is different for each version. By providing an operation ``add'' you can encapsulate these details from its actual use. In an application context you simply ``add two complex numbers'' regardless of how this functionality is actually archieved.
Once you have created an ADT for complex numbers, say Complex, you can use it in the same way like well-known data types such as integers.
Let's summarize this: The separation of data structures and operations and the constraint to only access the data structure via a well-defined interface allows you to choose data structures appropriate for the application environment.
ADTs are used to define a new type from which instances can be created. As shown in the list example, sometimes these instances should operate on other data types as well. For instance, one can think of lists of apples, cars or even lists. The semantical definition of a list is always the same. Only the type of the data elements change according to what type the list should operate on.
This additional information could be specified by a generic parameter which is specified at instance creation time. Thus an instance of a generic ADT is actually an instance of a particular variant of the ADT. A list of apples can therefore be declared as follows:
List<Apple> listOfApples;
The angle brackets now enclose the data type for which a variant of the generic ADT List should be created. listOfApples offers the same interface as any other list, but operates on instances of type Apple.
As ADTs provide an abstract view to describe properties of sets of entities, their use is independent from a particular programming language. We therefore introduce a notation here which is adopted from [3]. Each ADT description consists of two parts:
As an example the description of the ADT Integer is presented. Let k be an integer expression:
Consequently, the postcondition of this operation is sum = N+k. Don't confuse this with assign statements as used in programming languages! It is rather a mathematical equation which yields ``true'' for each value sum, N and k after add has been performed.
The description above is a specification for the ADT Integer. Please notice, that we use words for names of operations such as ``add''. We could use the more intuitive ``+'' sign instead, but this may lead to some confusion: You must distinguish the operation ``+'' from the mathematical use of ``+'' in the postcondition. The name of the operation is just syntax whereas the semantics is described by the associated pre- and postconditions. However, it is always a good idea to combine both to make reading of ADT specifications easier.
Real programming languages are free to choose an arbitrary implementation for an ADT. For example, they might implement the operation add with the infix operator ``+'' leading to a more intuitive look for addition of integers.
ADTs allows the creation of instances with well-defined properties and behaviour. In object-orientation ADTs are referred to as classes. Therefore a class defines properties of objects which are the instances in an object-oriented environment.
ADTs define functionality by putting main emphasis on the involved data, their structure, operations as well as axioms and preconditions. Consequently, object-oriented programming is ``programming with ADTs'': combining functionality of different ADTs to solve a problem. Therefore instances (objects) of ADTs (classes) are dynamically created, destroyed and used.
The previous sections already introduce some ``object-oriented'' concepts. However, they were applied in an procedural environment or in a verbal manner. In this section we investigate these concepts in more detail and give them names as used in existing object-oriented programming languages.
The last section introduces abstract data types (ADTs) as an abstract view to define properties of a set of entities. Object-oriented programming languages must allow to implement these types. Consequently, once an ADT is implemented we have a particular representation of it available.
Consider again the ADT Integer. Programming languages such as Pascal, C, Modula-2 and others already offer an implementation for it. Sometimes it is called int or integer. Once you've created a variable of this type you can use its provided operations. For example, you can add two integers:
int i, j, k; /* Define three integers */ i = 1; /* Assign 1 to integer i */ j = 2; /* Assign 2 to integer j */ k = i + j; /* Assign the sum of i and j to k */
Let's play with the above code fragment and outline the relationship to the ADT Integer. The first line defines three instances i, j and k of type Integer. Consequently, for each instance the special operation constructor should be called. In our example, this is internally done by the compiler. The compiler reserves memory to hold the value of an integer and ``binds'' the corresponding name to it. If you refer to i you actually refer to this memory area which was ``constructed'' by the definition of i. Optionally, compilers might choose to initialize the memory, for example, they might set it to 0 (zero).
The next line
i = 1;
sets the value of i to be 1. Therefore we can describe this line with help of the ADT notation as follows:
Perform operation set with argument 1 on the Integer instance
i. This is written as follows: i.set(1).
We now have a representation at two levels. The first level is the ADT level
where we express everything that is done to an instance of this ADT by the
invocation of
defined operations. At this level, pre- and postconditions are used to
describe what actually happens. In the following example, these conditions are
enclosed in curly brackets.
{ Precondition: i = n where n is any Integer }
i.set(1)
{ Postcondition: i = 1 }
Don't forget that we currently talk about the ADT level! Consequently, the
conditions are mathematical conditions.
The second level is the implementation level, where an actual representation is chosen for the operation. In C the equal sign ``='' implements the set() operation. However, in Pascal the following representation was chosen:
i := 1;
In either case, the ADT operation set is implemented.
Let's stress these levels a little bit further and have a look at the line
k = i + j;
Obviously, ``+'' was chosen to implement the add operation. We could read the part ``i + j'' as ``add the value of j to the value of i'', thus at the ADT level this results in
{ Precondition: Let i = n1 and j = n2 with n1,
n2 particular Integers }
i.add(j)
{ Postcondition: i = n1 and j = n2 }
The postcondition ensures that i and j do not change their values.
Please recall the specification of add. It says that a new Integer
is created the value of which is the sum. Consequently, we must provide a
mechanism to access this new instance. We do this with the set operation
applied on instance k:
{ Precondition: Let k = n where n is any Integer }
k.set(i.add(j))
{ Postcondition: k = i + j }
As you can see, some programming languages choose a representation which
almost equals the mathematical formulation used in the pre- and
postconditions. This makes it sometimes difficult to not mix up both levels.
class Integer {
attributes:
int i
methods:
setValue(int n)
Integer addValue(Integer j)
}
In the example above as well as in examples which follow we use a notation which is not programming language specific. In this notation class {...} denotes the definition of a class. Enclosed in the curly brackets are two sections attributes: and methods: which define the implementation of the data structure and operations of the corresponding ADT. Again we distinguish the two levels with different terms: At the implementation level we speak of ``attributes'' which are elements of the data structure at the ADT level. The same applies to ``methods'' which are the implementation of the ADT operations.
In
our example, the data structure consists of only one element: a signed
sequence of digits. The corresponding attribute is an ordinary integer of a
programming language![[*]](foot.gif) . We only define two methods setValue()
and addValue() representing the two operations set and add.
. We only define two methods setValue()
and addValue() representing the two operations set and add.
Definition (Class) A class is the implementation of an abstract
data
type (ADT). It defines attributes and methods which implement
the data structure and operations of the ADT, respectively.
Objects are uniquely identifiable by a name. Therefore you could have two distinguishable objects with the same set of values. This is similar to ``traditional'' programming languages where you could have, say two integers i and j both of which equal to ``2''. Please notice the use of ``i'' and ``j'' in the last sentence to name the two integers. We refer to the set of values at a particular time as the state of the object.
Definition (Object) An object is an instance of a class. It
can be uniquely identified by its name and it defines a
state which is represented by the values of its attributes at a particular
time.
The state of the object changes according to the methods which are applied to it. We refer to these possible sequence of state changes as the behaviour of the object:
Definition (Behaviour) The behaviour of an object is defined by
the set of methods which can be applied on it.
We now have two main concepts of object-orientation introduced, class and object. Object-oriented programming is therefore the implementation of abstract data types or, in more simple words, the writing of classes. At runtime instances of these classes, the objects, achieve the goal of the program by changing their states. Consequently, you can think of your running program as a collection of objects. The question arises of how these objects interact? We therefore introduce the concept of a message in the next section.
Integer i; /* Define a new integer object */ i.setValue(1); /* Set its value to 1 */
to express the fact, that the integer object i should set its value to
1. This is the message ``Apply method setValue with argument 1 on
yourself.'' sent to object i. We notate the sending of a message with
``.''. This notation is also used in C++; other object-oriented languages
might use other notations, for example ``-![]() ''.
''.
Sending a message asking an object to apply a method is similar to a procedure call in ``traditional'' programming languages. However, in object-orientation there is a view of autonomous objects which communicate with each other by exchanging messages. Objects react when they receive messages by applying methods on themselves. They also may deny the execution of a method, for example if the calling object is not allowed to execute the requested method.
In our example, the message and the method which should be applied once the message is received have the same name: We send ``setValue with argument 1'' to object i which applies ``setValue(1)''.
Definition (Message) A message is a request to an object to
invoke one of its methods. A
message therefore contains
Consequently, invocation of a method is just a reaction caused by receipt of a message. This is only possible, if the method is actually known to the object.
Definition (Method)
A method is associated with a class. An object invokes a method as a
reaction to receipt of a message.
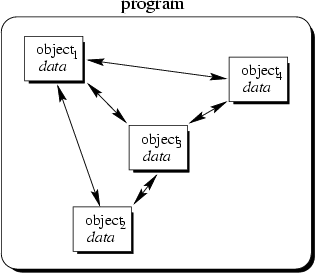
To view a program as a collection of interacting objects is a fundamental principle in object-oriented programming. Objects in this collection react upon receipt of messages, changing their state according to invocation of methods which might cause other messages sent to other objects. This is illustrated in Figure 4.1.
In this figure, the program consists of only four objects. These objects send messages to each other, as indicated by the arrowed lines. Note that the third object sends itself a message.
How does this view help us developing software? To answer this question let's recall how we have developed software for procedural programming languages. The first step was to divide the problem into smaller manageable pieces. Typically these pieces were oriented to the procedures which were taken place to solve the problem, rather than the involved data.
As an example consider your computer. Especially, how a character appears on the screen when you type a key. In a procedural environment you write down the several steps necessary to bring a character on the screen:
You do not distinguish entities with well-defined properties and well-known behaviour. In an object-oriented environment you would distinguish the interacting objects key and screen. Once a key receive a message that it should change its state to be pressed, its corresponding object sends a message to the screen object. This message requests the screen object to display the associated key value.
Whereas the previous lecture introduces the fundamental concepts of
object-oriented programming, this lecture presents more details about the
object-oriented idea. This section is mainly adopted from
[2]![[*]](foot.gif) .
.
In exercise 3.6.5 you already investigate relationships between abstract data types and instances and describe them in your own words. Let's go in more detail here.
Consider you have to write a drawing program. This program would allow drawing of various objects such as points, circles, rectangles, triangles and many more. For each object you provide a class definition. For example, the point class just defines a point by its coordinates:
class Point {
attributes:
int x, y
methods:
setX(int newX)
getX()
setY(int newY)
getY()
}
You continue defining classes of your drawing program with a class to describe circles. A circle defines a center point and a radius:
class Circle {
attributes:
int x, y,
radius
methods:
setX(int newX)
getX()
setY(int newY)
getY()
setRadius(newRadius)
getRadius()
}
Comparing both class definitions we can observe the following:
Knowing the properties of class Point we can describe a circle as a point plus a radius and methods to access it. Thus, a circle is ``a-kind-of'' point. However, a circle is somewhat more ``specialized''. We illustrate this graphically as shown in Figure 5.1.
In this and the following figures, classes are drawn using rectangles. Their name always starts with an uppercase letter. The arrowed line indicates the direction of the relation, hence, it is to be read as ``Circle is a-kind-of Point.''
The previous relationship is used at the class level to describe relationships between two similar classes. If we create objects of two such classes we refer to their relationship as an ``is-a'' relationship.
Since the class Circle is a kind of class Point, an instance of
Circle, say acircle, is a point![[*]](foot.gif) . Consequently, each circle behaves
like a point. For example, you can move points in x direction by
altering the value of x. Similarly, you move circles in this direction
by altering their x value.
. Consequently, each circle behaves
like a point. For example, you can move points in x direction by
altering the value of x. Similarly, you move circles in this direction
by altering their x value.
Figure 5.2 illustrates this relationship. In this and the following figures, objects are drawn using rectangles with round corners. Their name only consists of lowercase letters.
You sometimes need to be able to build objects by combining them out of others. You already know this from procedural programming, where you have the structure or record construct to put data of various types together.
Let's come back to our drawing program. You already have created several classes for the available figures. Now you decide that you want to have a special figure which represents your own logo which consists of a circle and a triangle. (Let's assume, that you already have defined a class Triangle.) Thus, your logo consists of two parts or the circle and triangle are part-of your logo:
class Logo {
attributes:
Circle circle
Triangle triangle
methods:
set(Point where)
}
We illustrate this in Figure 5.3.
This relationship is just the inverse version of the part-of relationship. Therefore we can easily add this relationship to the part-of illustration by adding arrows in the other direction (Figure 5.4).
With inheritance we are able to make use of the a-kind-of and is-a relationship. As described there, classes which are a-kind-of another class share properties of the latter. In our point and circle example, we can define a circle which inherits from point:
class Circle inherits from Point {
attributes:
int radius
methods:
setRadius(int newRadius)
getRadius()
}
Class Circle inherits all data elements and methods from point. There is no need to define them twice: We just use already existing and well-known data and method definitions.
On the object level we are now able to use a circle just as we would use a point, because a circle is-a point. For example, we can define a circle object and set its center point coordinates:
Circle acircle acircle.setX(1) /* Inherited from Point */ acircle.setY(2) acircle.setRadius(3) /* Added by Circle */
``Is-a'' also implies, that we can use a circle everywhere where a point is expected. For example, you can write a function or method, say move(), which should move a point in x direction:
move(Point apoint, int deltax) {
apoint.setX(apoint.getX() + deltax)
}
As a circle inherits from a point, you can use this function with a circle argument to move its center point and, hence, the whole circle:
Circle acircle
...
move(acircle, 10) /* Move circle by moving */
/* its center point */
Let's try to formalize the term ``inheritance'':
Definition (Inheritance)
Inheritance is the mechanism which allows a class A to inherit
properties of a class B. We say ``A inherits from B''. Objects of class A
thus have access to attributes and
methods of class B without the need to redefine them.
Definition (Superclass/Subclass) If class A inherits from class B, then
B is called superclass
of A. A is called subclass of B.
In the literature you may also find other terms for ``superclass'' and ``subclass''. Superclasses are also called parent classes. Subclasses may also be called child classes or just derived classes.
Of course, you can again inherit from a subclass, making this class the superclass of the new subclass. This leads to a hierarchy of superclass/subclass relationships. If you draw this hierarchy you get an inheritance graph.
A common drawing scheme is to use arrowed lines to indicate the inheritance relationship between two classes or objects. In our examples we have used ``inherits-from''. Consequently, the arrowed line starts from the subclass towards the superclass as illustrated in Figure 5.5.
In the literature you also find illustrations where the arrowed lines are used just the other way around. The direction in which the arrowed line is used, depends on how the corresponding author has decided to understand it.
Anyway, within this tutorial, the arrowed line is always directed towards the superclass.
In the following sections an unmarked arrowed line indicates ``inherit-from''.
One important object-oriented mechanism is multiple inheritance. Multiple inheritance does not mean that multiple subclasses share the same superclass. It also does not mean that a subclass can inherit from a class which itself is a subclass of another class.
Multiple inheritance means that one subclass can have more than one superclass. This enables the subclass to inherit properties of more than one superclass and to ``merge'' their properties.
As an example consider again our drawing program. Suppose we already have a class String which allows convenient handling of text. For example, it might have a method to append other text. In our program we would like to use this class to add text to the possible drawing objects. It would be nice to also use already existing routines such as move() to move the text around. Consequently, it makes sense to let a drawable text have a point which defines its location within the drawing area. Therefore we derive a new class DrawableString which inherits properties from Point and String as illustrated in Figure 5.6.
In our pseudo language we write this by simply separating the multiple superclasses by comma:
class DrawableString inherits from Point, String {
attributes:
/* All inherited from superclasses */
methods:
/* All inherited from superclasses */
}
We can use objects of class DrawableString like both points and strings. Because a drawablestring is-a point we can move them around
DrawableString dstring ... move(dstring, 10) ...
Since it is a string, we can append other text to them:
dstring.append("The red brown fox ...")
Now it's time for the definition of multiple inheritance:
Definition (Multiple Inheritance)
If class A inherits from more than one class, ie. A inherits from B1,
B2, ..., Bn, we speak of multiple inheritance. This may introduce
naming conflicts in A if at least two of its superclasses define
properties with the same name.
The above definition introduce naming conflicts which occur if more than
one superclass of a subclass use the same name for either attributes or
methods. For an example, let's assume, that class String defines a
method setX() which sets the string to a sequence of ``X''
characters![[*]](foot.gif) . The question arises,
what should be inherited by DrawableString? The Point,
String version or none of them?
. The question arises,
what should be inherited by DrawableString? The Point,
String version or none of them?
These conflicts can be solved in at least two ways:
The first solution is not very convenient as it introduces implicit consequences depending on the order in which classes inherit from each other. For the second case, subclasses must explicitly redefine properties which are involved in a naming conflict.
A special type of naming conflict is introduced if a class D multiply inherits from superclasses B and C which themselves are derived from one superclass A. This leads to an inheritance graph as shown in Figure 5.7.
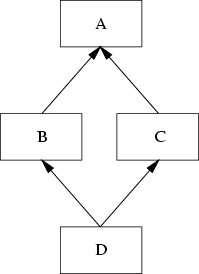 |
The question arises what properties class D actually inherits from its superclasses B and C. Some existing programming languages solve this special inheritance graph by deriving D with
Consequently, D cannot introduce naming conflicts with names of class A. However, if B and C add properties with the same name, D runs into a naming conflict.
Another possible solution is, that D inherits from both inheritance paths. In this solution, D owns two copies of the properties of A: one is inherited by B and one by C.
Although multiple inheritance is a powerful object-oriented mechanism the problems introduced with naming conflicts have lead several authors to ``doom'' it. As the result of multiple inheritance can always be achieved by using (simple) inheritance some object-oriented languages even don't allow its use. However, carefully used, under some conditions multiple inheritance provides an efficient and elegant way of formulating things.
With inheritance we are able to force a subclass to offer the same properties like their superclasses. Consequently, objects of a subclass behave like objects of their superclasses.
Sometimes it make sense to only describe the properties of a set of objects without knowing the actual behaviour beforehand. In our drawing program example, each object should provide a method to draw itself on the drawing area. However, the necessary steps to draw an objects depends on its represented shape. For example, the drawing routine of a circle is different from the drawing routine of a rectangle.
Let's call the drawing method print(). To force every drawable object to include such method, we define a class DrawableObject from which every other class in our example inherits general properties of drawable objects:
abstract class DrawableObject {
attributes:
methods:
print()
}
We introduce the new keyword abstract here. It is used to express the fact that derived classes must ``redefine'' the properties to fulfill the desired functionality. Thus from the abstract class' point of view, the properties are only specified but not fully defined. The full definition including the semantics of the properties must be provided by derived classes.
Now, every class in our drawing program example inherits properties from the general drawable object class. Therefore, class Point changes to:
class Point inherits from DrawableObject {
attributes:
int x, y
methods:
setX(int newX)
getX()
setY(int newY)
getY()
print() /* Redefine for Point */
}
We are now able to force every drawable object to have a method called print which should provide functionality to draw the object within the drawing area. The superclass of all drawable objects, class DrawableObject, does not provide any functionality for drawing itself. It is not intended to create objects from it. This class rather specifies properties which must be defined by every derived class. We refer to this special type of classes as abstract classes:
Definition (Abstract Class)
A class A is called abstract class if it is only used as a superclass
for other classes. Class A only specifies properties. It is not used to create
objects. Derived classes must define the
properties of A.
Abstract classes allow us to structure our inheritance graph. However, we actually don't want to create objects from them: we only want to express common characteristics of a set of classes.
A corresponding definition might look like this:
class Sphere inherits from Circle {
attributes:
int z /* Add third dimension */
methods:
setZ(int newZ)
getZ()
}
Give reasons for advantages/disadvantages of this alternative.
What naming conflicts can occur? Try to define cases by playing with simple example classes.
We continue with our tour through the world of object-oriented concepts by presenting a short introduction to static versus dynamic binding. With this, we can introduce polymorphism as a mechanism which let objects figure out what to do at runtime. But first, here is a brief overview about generic types.
We already know generic types from chapter 3 when we have talked about generic abstract data types. When defining a class, we actually define a user defined type. Some of these types can operate on other types. For example, there could be lists of apples, list of cars, lists of complex numbers of even lists of lists.
At the time, when we write down a class definition, we must be able to say that this class should define a generic type. However, we don't know with which types the class will be used. Consequently, we must be able to define the class with help of a ``placeholder'' to which we refer as if it is the type on which the class operates. Thus, the class definition provides us with a template of an actual class. The actual class definition is created once we declare a particular object. Let's illustrate this with the following example. Suppose, you want to define a list class which should be a generic type. Thus, it should be possible to declare list objects for apples, cars or any other type.
template class List for T {
attributes:
... /* Data structure needed to implement */
/* the list */
methods:
append(T element)
T getFirst()
T getNext()
bool more()
}
The above template class List looks like any other class definition. However, the first line declares List to be a template for various types. The identifier T is used as a placeholder for an actual type. For example, append() takes one element as an argument. The type of this element will be the data type with which an actual list object is created. For example, we can declare a list object for apples if a definition fot the type Apple exists:
List for Apple appleList
Apple anApple,
anotherApple
appleList.append(anotherApple)
appleList.append(anApple)
The first line declares appleList to be a list for apples. At this time, the compiler uses the template definition, substitutes every occurrence of T with Apple and creates an actual class definition for it. This leads to a class definition similar to the one that follows:
class List {
attributes:
... /* Data structure needed to implement */
/* the list */
methods:
append(Apple element)
Apple getFirst()
Apple getNext()
bool more()
}
This is not exactly, what the compiler generates. The compiler must ensure that we can create multiple lists for different types at any time. For example, if we need another list for, say pears, we can write:
List for Apple appleList List for Pear pearList ...
In both cases the compiler generates an actual class definition. The reason why both do not conflict by their name is that the compiler generates unique names. However, since this is not viewable to us, we don't go in more detail here. In any case, if you declare just another list of apples, the compiler can figure out if there already is an actual class definition and use it or if it has to be created. Thus,
List for Apple aList List for Apple anotherList
will create the actual class definition for aList and will reuse it for anotherList. Consequently, both are of the same type. We summarize this in the following definition:
Definition (Template Class)
If a class A is parameterized with a data type B, A is called template
class. Once an object of A is created, B is replaced by an actual data
type. This allows the definition of an actual class based on the
template specified for A and the actual data type.
We are able to define template classes with more than one parameter. For example, directories are collections of objects where each object can be referenced by a key. Of course, a directory should be able to store any type of object. But there are also various possibilities for keys. For instance, they might be strings or numbers. Consequently, we would define a template class Directory which is based on two type parameters, one for the key and one for the stored objects.
In strongly typed programming languages you typically have to declare variables prior to their use. This also implies the variable's definition where the compiler reserves space for the variable. For example, in Pascal an expression like
var i : integer;
declares variable i to be of type integer. Additionally, it defines enough memory space to hold an integer value.
With the declaration we bind the name i to the type integer. This binding is true within the scope in which i is declared. This enables the compiler to check at compilation time for type consistency. For example, the following assignment will result in a type mismatch error when you try to compile it:
var i : integer; ... i := 'string';
We call this particular type of binding ``static'' because it is fixed at compile time.
Definition (Static Binding)
If the type T of a variable is explicitly associated with its name N by
declaration, we say, that N is statically bound to T. The association
process is called static binding.
There exist programming languages which are not using explicitly typed variables. For example, some languages allow to introduce variables once they are needed:
... /* No appearance of i */ i := 123 /* Creation of i as an integer */
The type of i is known as soon as its value is set. In this case, i is of type integer since we have assigned a whole number to it. Thus, because the content of i is a whole number, the type of i is integer.
Definition (Dynamic Binding)
If the type T of a variable with name N is implicitly associated by its
content, we say, that N is dynamically bound to T. The association
process is called dynamic binding.
Both bindings differ in the time when the type is bound to the variable. Consider the following example which is only possible with dynamic binding:
if somecondition() == TRUE then
n := 123
else
n := 'abc'
endif
The type of n after the if statement depends on the evaluation of somecondition(). If it is TRUE, n is of type integer whereas in the other case it is of type string.
The first type is similar to the concept of dynamic binding. Here, the type of a variable depends on its content. Thus, its type depends on the content at a specific time:
v := 123 /* v is integer */ ... /* use v as integer */ v := 'abc' /* v "switches" to string */ ... /* use v as string */
Definition (Polymorphism (1))
The concept of dynamic binding allows a variable to take different types
dependent on the content at a particular time. This ability of a variable is
called polymorphism.
boolean isNull(int i) {
if (i == 0) then
return TRUE
else
return FALSE
endif
}
However, if we want to check this for real numbers, we should use another comparison due to the precision problem:
boolean isNull(real r) {
if (r < 0.01 and r > -0.99) then
return TRUE
else
return FALSE
endif
}
In both cases we want the function to have the name isNull. In programming languages without polymorphism for functions we cannot declare these two functions because the name isNull would be doubly defined. Without polymorphism for functions, doubly defined names would be ambiguous. However, if the language would take the parameters of the function into account it would work. Thus, functions (or methods) are uniquely identified by:
Since the parameter list of both isNull functions differ, the compiler is able to figure out the correct function call by using the actual types of the arguments:
var i : integer var r : real i = 0 r = 0.0 ... if (isNull(i)) then ... /* Use isNull(int) */ ... if (isNull(r)) then ... /* Use isNull(real) */
Definition (Polymorphism (2))
If a function (or method) is defined by the combination of
we speak of polymorphism.
This type of polymorphism allows us to reuse the same name for functions (or
methods) as long as the parameter list differs. Sometimes this type of
polymorphism is called overloading.
The last type of polymorphism allows an object to choose correct methods. Consider the function move() again, which takes an object of class Point as its argument. We have used this function with any object of derived classes, because the is-a relation holds.
Now consider a function display() which should be used to display drawable objects. The declaration of this function might look like this:
display(DrawableObject o) {
...
o.print()
...
}
We would like to use this function with objects of classes derived from DrawableObject:
Circle acircle Point apoint Rectangle arectangle display(apoint) /* Should invoke apoint.print() */ display(acircle) /* Should invoke acircle.print() */ display(arectangle) /* Should invoke arectangle.print() */
The actual method should be defined by the content of the object o of function display(). Since this is somewhat complicated, here is a more abstract example:
class Base {
attributes:
methods:
virtual foo()
bar()
}
class Derived inherits from Base {
attributes:
methods:
virtual foo()
bar()
}
demo(Base o) {
o.foo()
o.bar()
}
Base abase
Derived aderived
demo(abase)
demo(aderived)
In this example we define two classes Base and Derived. Each class defines two methods foo() and bar(). The first method is defined as virtual. This means that if this method is invoked its definition should be evaluated by the content of the object.
We then define a function demo() which takes a Base object as its argument. Consequently, we can use this function with objects of class Derived as the is-a relation holds. We call this function with a Base object and a Derived object, respectively.
Suppose, that foo() and bar() are defined to just print out their name and the class in which they are defined. Then the output is as follows:
foo() of Base called. bar() of Base called. foo() of Derived called. bar() of Base called.
Why is this so? Let's see what happens. The first call to demo() uses a Base object. Thus, the function's argument is ``filled'' with an object of class Base. When it is time to invoke method foo() it's actual functionality is chosen based on the current content of the corresponding object o. This time, it is a Base object. Consequently, foo() as defined in class Base is called.
The call to bar() is not subject to this content resolution. It is not marked as virtual. Consequently, bar() is called in the scope of class Base.
The second call to demo() takes a Derived object as its argument. Thus, the argument o is filled with a Derived object. However, o itself just represents the Base part of the provided object aderived.
Now, the call to foo() is evaluated by examining the content of o, hence, it is called within the scope of Derived. On the other hand, bar() is still evaluated within the scope of Base.
Definition (Polymorphism (3))
Objects of superclasses can be filled with objects of their subclasses.
Operators and methods of subclasses can be defined to be evaluated in two
contextes:
The second type is called polymorphism.
This section is the first part of the introduction to C++. Here we focus on C from which C++ was adopted. C++ extends the C programming language with strong typing, some features and - most importantly - object-oriented concepts.
Developed in the late 1970s, C gained an huge success due to the development of UNIX which was almost entirely written in this language [4]. In contrast to other high level languages, C was written by programmers for programmers. Thus it allows sometimes, say, weird things which in other languages such as Pascal are forbidden due to its bad influence on programming style. Anyway, when used with some discipline, C is as good a language as any other.
The comment in C is enclosed in /* ... */. Comments cannot be nested.
Table 7.1 describes the built-in data types of C. The specified Size is measured in bytes on a 386 PC running Linux 1.2.13. The provided Domain is based on the Size value. You can obtain information about the size of a data type with the sizeof operator.
Variables of these types are defined simply by preceeding the name with the type:
int an_int; float a_float; long long a_very_long_integer;
With struct you can combine several different types together. In other languages this is sometimes called a record:
struct date_s {
int day, month, year;
} aDate;
The above definition of aDate is also the declaration of a structure called date_s. We can define other variables of this type by referencing the structure by name:
struct date_s anotherDate;
We do not have to name structures. If we omit the name, we just cannot reuse it. However, if we name a structure, we can just declare it without defining a variable:
struct time_s {
int hour, minute, second;
};
We are able to use this structure as shown for anotherDate. This is very similar to a type definition known in other languages where a type is declared prior to the definition of a variable of this type.
Variables must be defined prior to their use. These definitions must occur before any statement, thus they form the topmost part within a statement block.
C defines all usual flow control statements. Statements are terminated by a semicolon ``;''. We can group multiple statements into blocks by enclosing them in curly brackets. Within each block, we can define new variables:
{
int i; /* Define a global i */
i = 1; /* Assign i the value 0 */
{ /* Begin new block */
int i; /* Define a local i */
i = 2; /* Set its value to 2 */
} /* Close block */
/* Here i is again 1 from the outer block */
}
Table 7.2 lists all flow control statements:
The for statement is the only statement which really differs from for statements known from other languages. All other statements more or less only differ in their syntax. What follows are two blocks which are totally equal in their functionality. One uses the while loop while the other the for variant:
{
int ix, sum;
sum = 0;
ix = 0; /* initialization */
while (ix < 10) { /* condition */
sum = sum + 1;
ix = ix + 1; /* step */
}
}
{
int ix, sum;
sum = 0;
for (ix = 0; ix < 10; ix = ix + 1)
sum = sum + 1;
}
To understand this, you have to know, that an assignment is an expression.
In C almost everything is an expression. For example, the assignment statement ``='' returns the value of its righthand operand. As a ``side effect'' it also sets the value of the lefthand operand. Thus,
ix = 12;
sets the value of ix to 12 (assuming that ix has an appropriate type). Now that the assignment is also an expression, we can combine several of them; for example:
kx = jx = ix = 12;
What happens? The first assignment assigns kx the value of its righthand side. This is the value of the assignment to jx. But this is the value of the assignment to ix. The value of this latter is 12 which is returned to jx which is returned to kx. Thus we have expressed
ix = 12; jx = 12; kx = 12;
in one line.
Truth in C is defined as follows. The value 0 (zero) stands for FALSE. Any other value is TRUE. For example, the standard function strcmp() takes two strings as argument and returns -1 if the first is lower than the second, 0 if they are equal and 1 if the first is greater than the second one. To compare if two strings str1 and str2 are equal you often see the following if construct:
if (!strcmp(str1, str2)) {
/* str1 equals str2 */
}
else {
/* str1 does not equal str2 */
}
The exclamation mark indicates the boolean NOT. Thus the expression evaluates to TRUE only if strcmp() returns 0.
Expressions are combined of both terms and operators. The first could be constansts, variables or expressions. From the latter, C offers all operators known from other languages. However, it offers some operators which could be viewed as abbreviations to combinations of other operators. Table 7.3 lists available operators. The second column shows their priority where smaller numbers indicate higher priority and same numbers, same priority. The last column lists the order of evaluation.
Most of these operators are already known to you. However, some need some more description. First of all notice that the binary boolean operators &, ^ and | are of lower priority than the equality operators == and !=. Consequently, if you want to check for bit patterns as in
if ((pattern & MASK) == MASK) {
...
}
you must enclose the binary operation into parenthesis![[*]](foot.gif) .
.
The increment operators ++ and ![]() can be explained by the
following example. If you have the following statement sequence
can be explained by the
following example. If you have the following statement sequence
a = a + 1; b = a;
you can use the preincrement operator
b = ++a;
Similarly, if you have the following order of statements:
b = a; a = a + 1;
you can use the postincrement operator
b = a++;
Thus, the preincrement operator first increments its associated variable and
then returns the new value, whereas the postincrement operator first returns
the
value and then increments its variable. The same rules apply to the pre- and
postdecrement operator ![]() .
.
Function calls, nested assignments and the increment/decrement operators cause side effects when they are applied. This may introduce compiler dependencies as the evaluation order in some situations is compiler dependent. Consider the following example which demonstrates this:
a[i] = i++;
The question is, whether the old or new value of i is used as the subscript into the array a depends on the order the compiler uses to evaluate the assignment.
The conditional operator ?: is an abbreviation for a commonly used if statement. For example to assign max the maximum of a and b we can use the following if statement:
if (a > b)
max = a;
else
max = b;
These types of if statements can be shorter written as
max = (a > b) ? a : b;
The next unusual operator is the operator assignment. We are often using assignments of the following form
expr1 = (expr1) op (expr2)
for example
i = i * (j + 1);
In these assignments the lefthand value also appears on the right side. Using informal speech we could express this as ``set the value of i to the current value of i multiplied by the sum of the value of j and 1''. Using a more natural way, we would rather say ``Multiply i with the sum of the value of j and 1''. C allows us to abbreviate these types of assignments to
i *= j + 1;
We can do that with almost all binary operators. Note, that the above operator assignment really implements the long form although ``j + 1'' is not in parenthesis.
The last unusal operator is the comma operator ,. It is best explained by an example:
i = 0; j = (i += 1, i += 2, i + 3);
This operator takes its arguments and evaluates them from left to right and returns the value of the rightmost expression. Thus, in the above example, the operator first evaluates ``i += 1'' which, as a side effect, increments the value of i. Then the next expression ``i += 2'' is evaluated which adds 2 to i leading to a value of 3. The third expression is evaluated and its value returned as the operator's result. Thus, j is assigned 6.
The comma operator introduces a particular pitfall when using
n-dimensional arrays with ![]() . A frequent error is to use a comma separated
list of indices to try to access an element:
. A frequent error is to use a comma separated
list of indices to try to access an element:
int matrix[10][5]; // 2-dim matrix int i; ... i = matrix[1,2]; // WON'T WORK!! i = matrix[1][2]; // OK
What actually happens in the first case is, that the comma separated list is interpreted as the comma operator. Consequently, the result is 2 which leads to an assignment of the address to the third five elements of the matrix!
Some of you might wonder, what C does with values which are not used. For example in the assignment statements we have seen before,
ix = 12; jx = 12; kx = 12;
we have three lines which each return 12. The answer is, that C ignores values which are not used. This leads to some strange things. For example, you could write something like this:
ix = 1; 4711; jx = 2;
But let's forget about these strange things. Let's come back to something more useful. Let's talk about functions.
As C is a procedural language it allows the definition of functions. Procedures are ``simulated'' by functions returning ``no value''. This value is a special type called void.
Functions are declared similar to variables, but they enclose their arguments in parenthesis (even if there are no arguments, the parenthesis must be specified):
int sum(int to); /* Declaration of sum with one argument */
int bar(); /* Declaration of bar with no arguments */
void foo(int ix, int jx);
/* Declaration of foo with two arguments */
To actually define a function, just add its body:
int sum(int to) {
int ix, ret;
ret = 0;
for (ix = 0; ix < to; ix = ix + 1)
ret = ret + ix;
return ret; /* return function's value */
} /* sum */
C only allows you to pass function arguments by value. Consequently you cannot change the value of one argument in the function. If you must pass an argument by reference you must program it on your own. You therefore use pointers.
One of the most common problems in programming in C (and sometimes C++) is the understanding of pointers and arrays. In C (C++) both are highly related with some small but essential differences. You declare a pointer by putting an asterisk between the data type and the name of the variable or function:
char *strp; /* strp is `pointer to char' */
You access the content of a pointer by dereferencing it using again the asterisk:
*strp = 'a'; /* A single character */
As in other languages, you must provide some space for the value to which the
pointer points. A pointer to characters can be used to point to a sequence
of characters: the string. Strings in C are terminated by a special
character NUL (0 or as char '![]() '). Thus, you can have
strings of any length. Strings are enclosed in double quotes:
'). Thus, you can have
strings of any length. Strings are enclosed in double quotes:
strp = "hello";
In this case, the compiler automatically adds the terminating NUL character. Now, strp points to a sequence of 6 characters. The first character is `h', the second `e' and so forth. We can access these characters by an index in strp:
strp[0] /* h */ strp[1] /* e */ strp[2] /* l */ strp[3] /* l */ strp[4] /* o */ strp[5] /* \0 */
The first character also equals ``*strp'' which can be written as ``*(strp + 0)''. This leads to something called pointer arithmetic and which is one of the powerful features of C. Thus, we have the following equations:
*strp == *(strp + 0) == strp[0]
*(strp + 1) == strp[1]
*(strp + 2) == strp[2]
...
Note that these equations are true for any data type. The addition is not oriented to bytes, it is oriented to the size of the corresponding pointer type!
The strp pointer can be set to other locations. Its destination may vary. In contrast to that, arrays are fix pointers. They point to a predefined area of memory which is specified in brackets:
char str[6];
You can view str to be a constant pointer pointing to an area of 6 characters. We are not allowed to use it like this:
str = "hallo"; /* ERROR */
because this would mean, to change the pointer to point to 'h'. We must copy the string into the provided memory area. We therefore use a function called strcpy() which is part of the standard C library.
strcpy(str, "hallo"); /* Ok */
Note however, that we can use str in any case where a pointer to a character is expected, because it is a (fixed) pointer.
Here we introduce the first program which is so often used: a program which prints ``Hello, world!'' to your screen:
#include <stdio.h>
/* Global variables should be here */
/* Function definitions should be here */
int
main() {
puts("Hello, world!");
return 0;
} /* main */
The first line looks something strange. Its explanation requires some information about how C (and C++) programs are handled by the compiler. The compilation step is roughly divided into two steps. The first step is called ``preprocessing'' and is used to prepare raw C code. In this case this step takes the first line as an argument to include a file called stdio.h into the source. The angle brackets just indicate, that the file is to be searched in the standard search path configured for your compiler. The file itself provides some declarations and definitions for standard input/output. For example, it declares a function called put(). The preprocessing step also deletes the comments.
In the second step the generated raw C code is compiled to an executable. Each executable must define a function called main(). It is this function which is called once the program is started. This function returns an integer which is returned as the program's exit status.
Function main() can take arguments which represent the command line parameters. We just introduce them here but do not explain them any further:
#include <stdio.h>
int
main(int argc, char *argv[]) {
int ix;
for (ix = 0; ix < argc; ix++)
printf("My %d. argument is %s\n", ix, argv[ix]);
return 0;
} /* main */
The first argument argc just returns the number of arguments given on the command line. The second argument argv is an array of strings. (Recall that strings are represented by pointers to characters. Thus, argv is an array of pointers to characters.)
This section is far from complete. We only want to give you an expression of what C is. We also want to introduce some basic concepts which we will use in the following section. Some concepts of C are improved in C++. For example, C++ introduces the concept of references which allow something similar to call by reference in function calls.
We suggest that you take your local compiler and start writing a few programs (if you are not already familiar with C, of course). One problem for beginners often is that existing library functions are unknown. If you have a UNIX system try to use the man command to get some descriptions. Especially you might want to try:
man gets man printf man puts man scanf man strcpy
We also suggest, that you get yourself a good book about C (or to find one of the on-line tutorials). We try to explain everything we introduce in the next sections. However, there is nothign wrong with having some reference at hand.
This section presents extensions to the C language which were introduced by C++ [6]. It also deals with object-oriented concepts and their realization.
C++ adds a new comment which is introduced by two slashes (//) and which lasts until the end of line. You can use both comment styles, for example to comment out large blocks of code:
/* C comment can include // and can span over
several lines. */
// /* This is the C++ style comment */ until end of line
In C you must define variables at the beginning of a block. C++ allows you to define variables and objects at any position in a block. Thus, variables and objects should be defined where they are used.
C++ introduces a new data type called reference. You can think of them as if they were ``aliases'' to ``real'' variables or objects. As an alias cannot exist without its corresponding real part, you cannot define single references. The ampersand (&) is used to define a reference. For example:
int ix; /* ix is "real" variable */ int &rx = ix; /* rx is "alias" for ix */ ix = 1; /* also rx == 1 */ rx = 2; /* also ix == 2 */
References can be used as function arguments and return values. This allows to pass parameters as reference or to return a ``handle'' to a calculated variable or object.
The table 8.1 is adopted from [1] and provides you with an overview of possible declarations. It is not complete in that it shows not every possible combination and some of them have not been introduced here, because we are not going to use them. However, these are the ones which you will probably use very often.
In C and C++ you can use the modifier const to declare particular aspects of a variable (or object) to be constant. The next table 8.2 lists possible combinations and describe their meaning. Subsequently, some examples are presented which demonstrate the use of const.
Now let's investigate some examples of contant variables and how to use them. Consider the following declarations (again from [1]):
int i; // just an ordinary integer
int *ip; // uninitialized pointer to
// integer
int * const cp = &i; // constant pointer to integer
const int ci = 7; // constant integer
const int *cip; // pointer to constant integer
const int * const cicp = &ci; // constant pointer to constant
// integer
The following assignments are valid:
i = ci; // assign constant integer to integer
*cp = ci; // assign constant integer to variable
// which is referenced by constant pointer
cip = &ci; // change pointer to constant integer
cip = cicp; // set pointer to constant integer to
// reference variable of constant pointer to
// constant integer
The following assignments are invalid:
ci = 8; // cannot change constant integer value
*cip = 7; // cannot change constant integer referenced
// by pointer
cp = &ci; // cannot change value of constant pointer
ip = cip; // this would allow to change value of
// constant integer *cip with *ip
When used with references some peculiarities must be considered. See the following example program:
#include <stdio.h>
int main() {
const int ci = 1;
const int &cr = ci;
int &r = ci; // create temporary integer for reference
// cr = 7; // cannot assign value to constant reference
r = 3; // change value of temporary integer
print("ci == %d, r == %d\n", ci, r);
return 0;
}
When compiled with GNU g++, the compiler issues the following warning:
What actually happens is, that the compiler automatically creates a temporay integer variable with value of ci to which reference r is initialized. Consequently, when changing r the value of the temporary integer is changed. This temporary variable lives as long as reference r.
Reference cr is defined as read-only (constant reference). This disables its use on the left side of assignments. You may want to remove the comment in front of the particular line to check out the resulting error message of your compiler.
C++ allows function overloading as defined in section 6.3. For example, we can define two different functions max(), one which returns the maximum of two integers and one which returns the maximum of two strings:
#include <stdio.h>
int max(int a, int b) {
if (a > b) return a;
return b;
}
char *max(char *a, char * b) {
if (strcmp(a, b) > 0) return a;
return b;
}
int main() {
printf("max(19, 69) = %d\n", max(19, 69));
printf("max(abc, def) = %s\n", max("abc", "def"));
return 0;
}
The above example program defines these two functions which differ in their parameter list, hence, they define two different functions. The first printf() call in function main() issues a call to the first version of max(), because it takes two integers as its argument. Similarly, the second printf() call leads to a call of the second version of max().
References can be used to provide a function with an alias of an actual function call argument. This enables to change the value of the function call argument as it is known from other languages with call-by-reference parameters:
void foo(int byValue, int &byReference) {
byValue = 42;
byReference = 42;
}
void bar() {
int ix, jx;
ix = jx = 1;
foo(ix, jx);
/* ix == 1, jx == 42 */
}
C++ allows the declaration and definition of classes. Instances of classes are called objects. Recall the drawing program example of section 5 again. There we have developed a class Point. In C++ this would look like this:
class Point {
int _x, _y; // point coordinates
public: // begin interface section
void setX(const int val);
void setY(const int val);
int getX() { return _x; }
int getY() { return _y; }
};
Point apoint;
This declares a class Point and defines an object apoint. You can think of a class definition as a structure definition with functions (or ``methods''). Additionally, you can specify the access rights in more detail. For example, _x and _y are private, because elements of classes are private as default. Consequently, we explicitly must ``switch'' the access rights to declare the following to be public. We do that by using the keyword public followed by a colon: Every element following this keyword are now accessible from outside of the class.
We can switch back to private access rights by starting a private section with private:. This is possible as often as needed:
class Foo {
// private as default ...
public:
// what follows is public until ...
private:
// ... here, where we switch back to private ...
public:
// ... and back to public.
};
Recall that a structure struct is a combination of various data elements which are accessible from the outside. We are now able to express a structure with help of a class, where all elements are declared to be public:
class Struct {
public: // Structure elements are public by default
// elements, methods
};
This is exactly what C++ does with struct. Structures are handled like classes. Whereas elements of classes (defined with class) are private by default, elements of structures (defined with struct) are public. However, we can also use private: to switch to a private section in structures.
Let's come back to our class Point. Its interface starts with the public section where we define four methods. Two for each coordinate to set and get its value. The set methods are only declared. Their actual functionality is still to be defined. The get methods have a function body: They are defined within the class or, in other words, they are inlined methods.
This type of method definition is useful for small and simple bodies. It also improve performance, because bodies of inlined methods are ``copied'' into the code wherever a call to such a method takes place.
On the contrary, calls to the set methods would result in a ``real'' function call. We define these methods outside of the class declaration. This makes it necessary, to indicate to which class a method definition belongs to. For example, another class might just define a method setX() which is quite different from that of Point. We must be able to define the scope of the definition; we therefore use the scope operator ``::'':
void Point::setX(const int val) {
_x = val;
}
void Point::setY(const int val) {
_y = val;
}
Here we define method setX() (setY()) within the scope of class Point. The object apoint can use these methods to set and get information about itself:
Point apoint; apoint.setX(1); // Initialization apoint.setY(1); // // x is needed from here, hence, we define it here and // initialize it to the x-coordinate of apoint // int x = apoint.getX();
The question arises about how the methods ``know'' from which object they are invoked. This is done by implicitly passing a pointer to the invoking object to the method. We can access this pointer within the methods as this. The definitions of methods setX() and setY() make use of class members _x and _y, respectively. If invoked by an object, these members are ``automatically'' mapped to the correct object. We could use this to illustrate what actually happens:
void Point::setX(const int val) {
this->_x = val; // Use this to reference invoking
// object
}
void Point::setY(const int val) {
this->_y = val;
}
Here we explicitly use the pointer this to explicitly dereference the invoking object. Fortunately, the compiler automatically ``inserts'' these dereferences for class members, hence, we really can use the first definitions of setX() and setY(). However, it sometimes make sense to know that there is a pointer this available which indicates the invoking object.
Currently, we need to call the set methods to initialize a point object![[*]](foot.gif) .
However, we would like to initialize the point when we define it. We therefore use
special methods called constructors.
.
However, we would like to initialize the point when we define it. We therefore use
special methods called constructors.
class Point {
int _x, _y;
public:
Point() {
_x = _y = 0;
}
void setX(const int val);
void setY(const int val);
int getX() { return _x; }
int getY() { return _y; }
};
Constructors have the same name of the class (thus they are identified to be constructors). They have no return value. As other methods, they can take arguments. For example, we may want to initialize a point to other coordinates than (0, 0). We therefore define a second constructor taking two integer arguments within the class:
class Point {
int _x, _y;
public:
Point() {
_x = _y = 0;
}
Point(const int x, const int y) {
_x = x;
_y = y;
}
void setX(const int val);
void setY(const int val);
int getX() { return _x; }
int getY() { return _y; }
};
Constructors are implicitly called when we define objects of their classes:
Point apoint; // Point::Point() Point bpoint(12, 34); // Point::Point(const int, const int)
With constructors we are able to initialize our objects at definition time as we have requested it in section 2 for our singly linked list. We are now able to define a class List where the constructors take care of correctly initializing its objects.
If we want to create a point from another point, hence, copying the properties of one object to a newly created one, we sometimes have to take care of the copy process. For example, consider the class List which allocates dynamically memory for its elements. If we want to create a second list which is a copy of the first, we must allocate memory and copy the individual elements. In our class Point we therefore add a third constructor which takes care of correctly copying values from one object to the newly created one:
class Point {
int _x, _y;
public:
Point() {
_x = _y = 0;
}
Point(const int x, const int y) {
_x = x;
_y = y;
}
Point(const Point &from) {
_x = from._x;
_y = from._y;
}
void setX(const int val);
void setY(const int val);
int getX() { return _x; }
int getY() { return _y; }
};
The third constructor takes a constant reference to an object of class Point as an argument and assigns _x and _y the corresponding values of the provided object.
This type of constructor is so important that it has its own name: copy constructor. It is highly recommended that you provide for each of your classes such a constructor, even if it is as simple as in our example. The copy constructor is called in the following cases:
Point apoint; // Point::Point() Point bpoint(apoint); // Point::Point(const Point &) Point cpoint = apoint; // Point::Point(const Point &)
With help of constructors we have fulfilled one of our requirements of implementation of abstract data types: Initialization at definition time. We still need a mechanism which automatically ``destroys'' an object when it gets invalid (for example, because of leaving its scope). Therefore, classes can define destructors.
void foo() {
List alist; // List::List() initializes to
// empty list.
... // add/remove elements
} // Destructor call!
Destruction of objects take place when the object leaves its scope of definition or is explicitly destroyed. The latter happens, when we dynamically allocate an object and release it when it is no longer needed.
Destructors are declared similar to constructors. Thus, they also use the name prefixed by a tilde (~ ) of the defining class:
class Point {
int _x, _y;
public:
Point() {
_x = _y = 0;
}
Point(const int x, const int y) {
_x = xval;
_y = yval;
}
Point(const Point &from) {
_x = from._x;
_y = from._y;
}
~Point() { /* Nothing to do! */ }
void setX(const int val);
void setY(const int val);
int getX() { return _x; }
int getY() { return _y; }
};
Destructors take no arguments. It is even invalid to define one, because destructors are implicitly called at destruction time: You have no chance to specify actual arguments.
This section concludes our introduction to C++. We introduce ``real'' object-oriented concepts and we answer the question, how a C++ program is actually written.
class Point3D : public Point {
int _z;
public:
Point3D() {
setX(0);
setY(0);
_z = 0;
}
Point3D(const int x, const int y, const int z) {
setX(x);
setY(y);
_z = z;
}
~Point3D() { /* Nothing to do */ }
int getZ() { return _z; }
void setZ(const int val) { _z = val; }
};
The type of inheritance influences the access rights to elements of the various superclasses. Using public inheritance, everything which is declared private in a superclass remains private in the subclass. Similarly, everything which is public remains public. When using private inheritance the things are quite different as is shown in table 9.1.
The leftmost column lists possible access rights for elements of classes. It also includes a third type protected. This type is used for elements which should be directly usable in subclasses but which should not be accessible from the outside. Thus, one could say elements of this type are between private and public elements in that they can be used within the class hierarchy rooted by the corresponding class.
The second and third column show the resulting access right of the elements of a superclass when the subclass is privately and publically derived, respectively.
When we create an object with
Point3D point(1, 2, 3);
the second constructor of Point3D is invoked. Prior to the execution of the constructor body, the constructor Point() is invoked, to initialize the point part of object point. Fortunately, we have defined a constructor which takes no arguments. This constructor initializes the 2D coordinates _x and _y to 0 (zero). As Point3D is only derived from Point there are no other constructor calls and the body of Point3D(const int, const int, const int) is executed. Here we invoke methods setX() and setY() to explicitly override the 2D coordinates. Subsequently, the value of the third coordinate _z is set.
This is very unsatisfactory as we have defined a constructor Point() which takes two arguments to initialize its coordinates to them. Thus we must only be able to tell, that instead of using the default constructor Point() the paramterized Point(const int, const int) should be used. We can do that by specifying the desired constructors after a single colon just before the body of constructor Point3D():
class Point3D : public Point {
...
public:
Point3D() { ... }
Point3D(
const int x,
const int y,
const int z) : Point(x, y) {
_z = z;
}
...
};
If we would have more superclasses we simply provide their constructor calls as a comma separated list. We also use this mechanism to create contained objects. For example, suppose that class Part only defines a constructor with one argument. Then to correctly create an object of class Compound we must invoke Part() with its argument:
class Compound {
Part part;
...
public:
Compound(const int partParameter) : part(partParameter) {
...
}
...
};
This dynamic initialization can also be used with built-in data types. For example, the constructors of class Point could be written as:
Point() : _x(0), _y(0) {}
Point(const int x, const int y) : _x(x), _y(y) {}
You should use this initialization method as often as possible, because it allows the compiler to create variables and objects correctly initialized instead of creating them with a default value and to use an additional assignment (or other mechanism) to set its value.
class DrawableString : public Point, public DrawableObject {
...
public:
DrawableString(...) :
Point(...),
DrawableObject(...) {
...
}
~DrawableString() { ... }
...
};
We will not use this type of inheritance in the remainder of this tutorial. Therefore we will not go into further detail here.
class DrawableObject {
public:
virtual void print();
};
Class DrawableObject defines a method print() which is virtual. We can derive from this class other classes:
class Point : public DrawableObject {
...
public:
...
void print() { ... }
};
Again, print() is a virtual method, because it inherits this property from DrawableObject. The function display() which is able to display any kind of drawable object, can then be defined as:
void display(const DrawableObject &obj) {
// prepare anything necessary
obj.print();
}
When using virtual methods some compilers complain if the corresponding class destructor is not declared virtual as well. This is necessary when using pointers to (virtual) subclasses when it is time to destroy them. As the pointer is declared as superclass normally its destructor would be called. If the destructor is virtual, the destructor of the actual referenced object is called (and then, recursively, all destructors of its superclasses). Here is an example adopted from [1]:
class Colour {
public:
virtual ~Colour();
};
class Red : public Colour {
public:
~Red(); // Virtuality inherited from Colour
};
class LightRed : public Red {
public:
~LightRed();
};
Using these classes, we can define a palette as follows:
Colour *palette[3]; palette[0] = new Red; // Dynamically create a new Red object palette[1] = new LightRed; palette[2] = new Colour;
The newly introduced operator new creates a new object of the specified type in dynamic memory and returns a pointer to it. Thus, the first new returns a pointer to an allocated object of class Red and assigns it to the first element of array palette. The elements of palette are pointers to Colour and, because Red is-a Colour the assignment is valid.
The contrary operator to new is delete which explicitly destroys an object referenced by the provided pointer. If we apply delete to the elements of palette the following destructor calls happen:
delete palette[0]; // Call destructor ~Red() followed by ~Colour() delete palette[1]; // Call ~LightRed(), ~Red() and ~Colour() delete palette[2]; // Call ~Colour()
The various destructor calls only happen, because of the use of virtual destructors. If we would have not declared them virtual, each delete would have only called ~ Colour() (because palette[i] is of type pointer to Colour).
class DrawableObject {
...
public:
...
virtual void print() = 0;
};
This class definition would force every derived class from which objects should be created to define a method print(). These method declarations are also called pure methods.
Pure methods must also be declared virtual, because we only want to use objects from derived classes. Classes which define pure methods are called abstract classes.
class Complex {
double _real,
_imag;
public:
Complex() : _real(0.0), _imag(0.0) {}
Complex(const double real, const double imag) :
_real(real), _imag(imag) {}
Complex add(const Complex op);
Complex mul(const Complex op);
...
};
We would then be able to use complex numbers and to ``calculate'' with them:
Complex a(1.0, 2.0), b(3.5, 1.2), c; c = a.add(b);
Here we assign c the sum of a and b. Although absolutely correct, it does not provide a convenient way of expression. What we would rather like to use is the well-known ``+'' to express addition of two complex numbers. Fortunately, C++ allows us to overload almost all of its operators for newly created types. For example, we could define a ``+'' operator for our class Complex:
class Complex {
...
public:
...
Complex operator +(const Complex &op) {
double real = _real + op._real,
imag = _imag + op._imag;
return(Complex(real, imag));
}
...
};
In this case, we have made operator + a member of class Complex. An expression of the form
c = a + b;
is translated into a method call
c = a.operator +(b);
Thus, the binary operator + only needs one argument. The first argument is implicitly provided by the invoking object (in this case a).
However, an operator call can also be interpreted as a usual function call, as in
c = operator +(a, b);
In this case, the overloaded operator is not a member of a class. It is rather defined outside as a normal overloaded function. For example, we could define operator + in this way:
class Complex {
...
public:
...
double real() { return _real; }
double imag() { return _imag; }
// No need to define operator here!
};
Complex operator +(Complex &op1, Complex &op2) {
double real = op1.real() + op2.real(),
imag = op1.imag() + op2.imag();
return(Complex(real, imag));
}
In this case we must define access methods for the real and imaginary parts because the operator is defined outside of the class's scope. However, the operator is so closely related to the class, that it would make sense to allow the operator to access the private members. This can be done by declaring it to be a friend of class Complex.
We can define functions or classes to be friends of a class to allow them direct access to its private data members. For example, in the previous section we would like to have the function for operator + to have access to the private data members _real and _imag of class Complex. Therefore we declare operator + to be a friend of class Complex:
class Complex {
...
public:
...
friend Complex operator +(
const Complex &,
const Complex &
);
};
Complex operator +(const Complex &op1, const Complex &op2) {
double real = op1._real + op2._real,
imag = op1._imag + op2._imag;
return(Complex(real, imag));
}
You should not use friends very often because they break the data hiding principle in its fundamentals. If you have to use friends very often it is always a sign that it is time to restructure your inheritance graph.
Roughly speaking, modules consist of two file types: interface descriptions and implementation files. To distinguish these types, a set of suffixes are used when compiling C and C++ programs. Table 9.2 shows some of them.
In this tutorial we will use .h for header files, .cc for C++ files
and .tpl for template definition files. Even if we are writing ``only''
C code, it makes sense to use .cc to force the compiler to treat it as
C++. This simplifies combination of both, since the internal mechanism of how
the compiler arrange names in the program differs between both
languages![[*]](foot.gif) .
.
![[*]](foot.gif) and translates
them into
object files
and translates
them into
object files![[*]](foot.gif) . Typical suffixes for that file type are .o or
.obj.
. Typical suffixes for that file type are .o or
.obj.
After successful compilation the set of object files is processed by a
linker. This program combine the files, add necessary libraries![[*]](foot.gif) and
creates an executable. Under UNIX this file is called a.out if not
other specified.
These steps are illustrated in Figure 9.1.
and
creates an executable. Under UNIX this file is called a.out if not
other specified.
These steps are illustrated in Figure 9.1.
With modern compilers both steps can be combined. For example, our small example programs can be compiled and linked with the GNU C++ compiler as follows (``example.cc'' is just an example name, of course):
gcc example.cc
To avoid the inclusion of multiple copies caused by mutual dependencies we use conditional coding. The preprocessor also defines conditional statements to check for various aspects of its processing. For example, we can check if a macro is already defined:
#ifndef MACRO #define MACRO /* define MACRO */ ... #endif
The lines between #ifndef and #endif are only included, if MACRO is not already defined. We can use this mechanism to prevent multiple copies:
/* ** Example for a header file which `checks' if it is ** already included. Assume, the name of the header file ** is `myheader.h' */ #ifndef __MYHEADER_H #define __MYHEADER_H /* ** Interface declarations go here */ #endif /* __MYHEADER_H */
__MYHEADER_H is a unique name for each header file. You might want to follow the convention of using the name of the file prefixed with two underbars. The first time the file is included, __MYHEADER_H is not defined, thus every line is included and processed. The first line just defines a macro called __MYHEADER_H. If accidentally the file should be included a second time (while processing the same input file), __MYHEADER_H is defined, thus everything leading up to the #endif is skipped.
void display(const DrawableObject obj);does not produce the desired output.
![[*]](foot.gif) or just templates
for short.
A class template looks like a normal class
definition, where some aspects are represented by placeholders. In the
forthcoming list example we use this mechanism to generate lists for various
data types:
or just templates
for short.
A class template looks like a normal class
definition, where some aspects are represented by placeholders. In the
forthcoming list example we use this mechanism to generate lists for various
data types:
template <class T>
class List : ... {
public:
...
void append(const T data);
...
};
In the first line we introduce the keyword template which starts every template declaration. The arguments of a template are enclosed in angle brackets.
Each argument specifies a placeholder in the following class definition. In
our example, we want class List to be defined for various data types.
One could say, that we want to define a class of lists![[*]](foot.gif) . In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
. In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
An actual list definition must now specify the type of the list. If we stick to the class expression used before, we have to create a class instance. From this class instance we can then create ``real'' object instances:
List<int> integerList;
Here we create a class instance of a List which takes integers as its data elements. We specify the type enclosed in angle brackets. The compiler now applies the provided argument ``int'' and automatically generates a class definition where the placeholder T is replaced by int, for example, it generates the following method declaration for append():
void append(const int data);
Templates can take more than one argument to provide more placeholders. For example, to declare a dictionary class which provides access to its data elements by a key, one can think of the following declaration:
template <class K, class T>
class Dictionary {
...
public:
...
K getKey(const T from);
T getData(const K key);
...
};
Here we use two placeholders to be able to use dictionaries for various key and data types.
Template arguments can also be used to generate parameterized class definitions. For example, a stack might be implemented by an array of data elements. The size of the array could be specified dynamically:
template <class T, int size>
class Stack {
T _store[size];
public:
...
};
Stack<int,128> mystack;
In this example, mystack is a stack of integers using an array of 128 elements. However, in the following we will not use parameterized classes.
A traversing strategy defines the order in which elements of the data structure are to be visited. It makes sense to separate the shape from traversing strategies, because some data structures can be traversed using various strategies.
Traversing of a data structure is implemented using iterators. Iterators guarantee to visit each data item of their associated data structure in a well defined order. They must provide at least the following properties:
Have a look at Figure 10.1, which shows a list consisting of four rectangles. Each rectangle has a bullet in its middle, the first three point to their right neighbour. Since the last rectangle have no right neighbour, there is no pointer.
First let's choose names for these building blocks. Talking of rectangles is not appropriate, because one can think of a figure using circles or triangles.
Within the scope of graphs the name node is used. A node contains a pointer to its successor. Thus, the list in the figure consists of nodes, each of which has exactly one pointer associated with it.
Three types of nodes can be distinguished:
Note that the nodes do not carry any content. This is because the bare data structure list consists only of nodes, which are strung together. Of course real applications need nodes, carrying some content. But in the sense of object-orientation this is a specialization of the nodes.
From the figure we can see, that a list can only be used with one traversing strategy: forward cursor. Initially, the head will be the first current element. The successor function simply follows the pointer of the current node. The termination function checks the current element to be the tail.
Note that it is not possible to go back nor to start in the middle of the list. The latter would contradict the requirement, that each element must be visited.
The next question is, what are the operations offered by a list? A list only defines two well known nodes head and tail. Let's have a deeper look to them.
A new node can be put-in-front of the list such that:
Similarly, a new node can easily be appended to the tail:
The inverse function to put in front is delete-from-front:
You should be able to figure out why there is no cheap inverse append function.
Finally, there exist three other cheap primitives, whose meaning is straight forward. Thus, we will not examine them any further. However, we present them here for completeness:
Have a look at the following declaration of class Node.
class Node {
Node *_right;
public:
Node(Node *right = NULL) : _right(right) {}
Node(const Node &val) : _right(val._right) {}
const Node *right() const { return _right; }
Node *&right() { return _right; }
Node &operator =(const Node &val) {
_right = val._right;
return *this;
}
const int operator ==(const Node &val) const {
return _right == val._right;
}
const int operator !=(const Node &val) const {
return !(*this == val);
}
};
A look to the first version of method right() contains a const just before the method body. When used in this position, const declares the method to be constant regarding the elements of the invoking object. Consequently, you are only allowed to use this mechanism in method declarations or definitions, respectively.
This type of const modifier is also used to check for overloading. Thus,
class Foo {
...
int foo() const;
int foo();
};
declare two different methods. The former is used in constant contexts whereas the second is used in variable contexts.
Although template class Node implements a simple node it seems to define plenty of functionality. We do this, because it is good practice to offer at least the following functionality for each defined data type:
The unequality operator ``!='' is implemented by using the definition of the equality operator. Recall, that this points to the invoking object, thus,
Node a, b; ... if (a != b) ...
would result in a call to operator !=() with this set to the address of a. We dereference this using the standard dereference operator ``*''. Now, *this is an object of class Node which is compared to another object using operator ==(). Consequently, the definition of operator ==() of class Node is used. Using the standard boolean NOT operator ``!'' we negate the result and obtain the truth value of operator !=().
The above methods should be available for each class you define. This ensures that you can use your objects as you would use any other objects, for example integers. If some of these methods make no sense for whatever reason, you should declare them in a private section of the class to explicitly mark them as not for public use. Otherwise the C++ compiler would substitute standard operators.
Obviously, real applications require the nodes to carry data. As mentioned above, this means to specialize the nodes. Data can be of any type, hence, we are using the template construct.
template <class T>
class DataNode : public Node {
T _data;
public:
DataNode(const T data, DataNode *right = NULL) :
Node(right), _data(data) {}
DataNode(const DataNode &val) :
Node(val), _data(val._data) {}
const DataNode *right() const {
return((DataNode *) Node::right());
}
DataNode *&right() { return((DataNode *&) Node::right()); }
const T &data() const { return _data; }
T &data() { return _data; }
DataNode &operator =(const DataNode &val) {
Node::operator =(val);
_data = val._data;
return *this;
}
const int operator ==(const DataNode &val) const {
return(
Node::operator ==(val) &&
_data == val._data);
}
const int operator !=(const DataNode &val) const {
return !(*this == val);
}
};
The above template DataNode simply specializes class Node to carry data of any type. It adds functionality to access its data element and also offers the same set of standard functionality: Copy Constructor, operator =() and operator ==(). Note, how we reuse functionality already defined by class Node.
template <class T>
class ListBase {
public:
virtual ~ListBase() {} // Force destructor to be
// virtual
virtual void flush() = 0;
virtual void putInFront(const T data) = 0;
virtual void append(const T data) = 0;
virtual void delFromFront() = 0;
virtual const T &getFirst() const = 0;
virtual T &getFirst() = 0;
virtual const T &getLast() const = 0;
virtual T &getLast() = 0;
virtual const int isEmpty() const = 0;
};
What we actually do is to describe the interface of every list by specifying the prototypes of required methods. We do that for every operation we have identified in section 10.3. Additionally, we also include a method flush() which allows us to delete all elements of a list.
For operations get-first and get-last we have declared two versions. One is for use in a constant context and the other in a variable context.
With this abstract class template we are able to actually define our list class template:
template <class T>
class List : public ListBase<T> {
DataNode<T> *_head, *_tail;
public:
List() : _head(NULL), _tail(NULL) {}
List(const List &val) : _head(NULL), _tail(NULL) {
*this = val;
}
virtual ~List() { flush(); }
virtual void flush();
virtual void putInFront(const T data);
virtual void append(const T data);
virtual void delFromFront();
virtual const T &getFirst() const { return _head->data(); }
virtual T &getFirst() { return _head->data(); }
virtual const T &getLast() const { return _tail->data(); }
virtual T &getLast() { return _tail->data(); }
virtual const int isEmpty() const { return _head == NULL; }
List &operator =(const List &val) {
flush();
DataNode<T> *walkp = val._head;
while (walkp) append(walkp->data());
return *this;
}
const int operator ==(const List &val) const {
if (isEmpty() && val.isEmpty()) return 1;
DataNode<T> *thisp = _head,
*valp = val._head;
while (thisp && valp) {
if (thisp->data() != valp->data()) return 0;
thisp = thisp->right();
valp = valp->right();
}
return 1;
}
const int operator !=(const List &val) const {
return !(*this == val);
}
friend class ListIterator<T>;
};
The constructors initialize the list's elements _head and _tail to NULL which is the NUL pointer in C and C++. You should know how to implement the other methods from your programming experience. Here we only present the implementation of method putInFront():
template <class T> void
List<T>::putInFront(const T data) {
_head = new DataNode<T>(data, _head);
if (!_tail) _tail = _head;
} /* putInFront */
If we define methods of a class template outside of its declaration, we must
also specify the template keyword. Again we use the new operator
to create a new data node dynamically. This operator allows initialization of
its created object with arguments enclosed in parenthesis. In the above
example, new creates a new instance of class DataNode![]() T
T![]() .
Consequently, the corresponding constructor is called.
.
Consequently, the corresponding constructor is called.
Also notice how we use placeholder T. If we would create a class
instance of class template List, say, List![]() int
int![]() this would
also cause creation of a class instance of class template DataNode, viz
DataNode
this would
also cause creation of a class instance of class template DataNode, viz
DataNode![]() int
int![]() .
.
The last line of the class template declaration declares class template ListIterator to be a friend of List. We want to separately define the list's iterator. However, it is closely related, thus, we allow it to be a friend.
In section 10.2 we have introduced the concept of iterators to traverse through a data structure. Iterators must implement three properties:
Generally speaking, the iterator successively returns data associated with the
current element. Obviously, there will be a method, say, current() which
implements this functionality. The return type of this method depends on the
type of data
stored in the particular data structure. For example, when iterating over
List![]() int
int![]() the return type should be int.
the return type should be int.
The successor function, say, succ(), uses additional information which
is stored in
structural elements of the data structure. In our list example, these are the
nodes which carry the data and a pointer to their right neighbour. The
type of the structural elements usually differs from that of the raw data.
Consider again our List![]() int
int![]() where succ() must use
DataNode
where succ() must use
DataNode![]() int
int![]() as structural elements.
as structural elements.
The termination condition is implemented by a method, say, terminate(), which returns TRUE if (and only if) all data elements of the associated data structure have been visited. As long as succ() can find an element not yet visited, this method returns FALSE.
Again we want to specify an abstract iterator class which defines properties of every iterator. The thoughts above lead to the following declaration:
template <class Data, class Element>
class Iterator {
protected:
Element _start,
_current;
public:
Iterator(const Element start) :
_start(start), _current(start) {}
Iterator(const Iterator &val) :
_start(val._start), _current(val._current) {}
virtual ~Iterator() {}
virtual const Data current() const = 0;
virtual void succ() = 0;
virtual const int terminate() const = 0;
virtual void rewind() { _current = _start; }
Iterator &operator =(const Iterator &val) {
_start = val._start;
_current = val._current;
return *this;
}
const int operator ==(const Iterator &val) const {
return(_start == val._start && _current == val._current);
}
const int operator !=(const Iterator &val) const {
return !(*this == val);
}
};
Again we use the template mechanism to allow the use of the iterator for any data structure which stores data of type Data and which uses structural elements of type Element. Each iterator ``knows'' a starting (structural) element and the current element. We make both accessible from derived classes because derived iterators need access to them to implement the following iterator properties. You should already understand how the constructors operate and why we force the destructor to be virtual.
Subsequently we specify three methods which should implement the three properties of an iterator. We also add a method rewind() which simply sets the current element to the start element. However, complex data structures (for example hash tables) might require more sophisticated rewind algorithms. For that reason we also specify this method to be virtual, allowing derived iterators to redefine it for their associated data structure.
The last step in the iterator implementation process is the declaration of the list iterator. This iterator is highly related to our class template List, for example, it is clear that the structural elements are class templates DataNode. The only ``open'' type is the one for the data. Once again, we use the template mechanism to provide list iterators for the different list types:
template <class T>
class ListIterator : public Iterator<T, DataNode<T> *> {
public:
ListIterator(const List<T> &list) :
Iterator<T, DataNode<T> *>(list._head) {}
ListIterator(const ListIterator &val) :
Iterator<T, DataNode<T> *>(val) {}
virtual const T current() const { return _current->data(); }
virtual void succ() { _current = _current->right(); }
virtual const int terminate() const {
return _current == NULL;
}
T &operator ++(int) {
T &tmp = _current->data();
succ();
return tmp;
}
ListIterator &operator =(const ListIterator &val) {
Iterator<T, DataNode<T> *>::operator =(val);
return *this;
}
};
The class template ListIterator is derived from Iterator. The type
of data is, of course, the type for which the list iterator is declared,
hence, we insert placeholder T for the iterator's data type Data.
The iteration process is achieved with help of the structural elements of type
DataNode. Obviously the starting element is the head of the list
_head which is of type DataNode![]() T
T![]() *. We choose this type for the
element type Element.
*. We choose this type for the
element type Element.
Note that the list iterator actually hides the details about the structural elements. This type highly depends on the implementation of the list. For example, if we would have chosen an array implementation, we may have used integers as structural elements where the current element is indicated by an array index.
The first constructor takes the list to traverse as its argument and
initializes its iterator portion accordingly. As each
ListIterator![]() T
T![]() is a friend of List
is a friend of List![]() T
T![]() it has access to the
list's private members. We use this to initialize the iterator to point to the
head of the list.
it has access to the
list's private members. We use this to initialize the iterator to point to the
head of the list.
We omit the destructor because we do not have any additional data members for the list iterator. Consequently, we do nothing special for it. However, the destructor of class template Iterator is called. Recall that we have to define this destructor to force derived classes to also have a virtual one.
The next methods just define the required three properties. Now that we have
structural elements defined as DataNode![]() T
T![]() * we use them as follows:
* we use them as follows:
We have also included an overloaded postincrement operator ``++''. To distinguish this operator from the preincrement operator, it takes an additional (anonymous) integer argument. As we only use this argument to declare a correct operator prototype and because we do not use the value of the argument, we omit the name of the argument.
The last method is the overloaded assignment operator for list
iterators. Similar to previous assignment operators, we just reuse already
defined assignments of superclasses; Iterator![]() T
T![]() ::operator =() in
this case.
::operator =() in
this case.
The other methods and operators, namely rewind(), operator ==() and operator !=() are all inherited from class template Iterator.
int
main() {
List<int> list;
int ix;
for (ix = 0; ix < 10; ix++) list.append(ix);
ListIterator<int> iter(list);
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
puts("");
return 0;
}
As we have defined a postincrement operator for the list iterator, the loop can also be written as:
while (!iter.terminate())
print("%d ", iter++);
The presented example focusses on an object-oriented view. In real applications singly linked lists might offer more functionality. For example, insertion of new data items should be no problem due to the use of pointers:
Two simple operations. However, the problem is to designate the element after which the new element should be inserted. Again, a mechanism is needed which traverse through the list. This time, however, traversion stops at a particular element: It is the element where the list (or the data structure) is modified.
Similar to the existence of different traversing strategies, one can think of different modification strategies. For example, to create a sorted list, where elements are sorted in ascending order, use an ascending modifier.
These modifiers must have access to the list structural elements, and thus, they would be declared as friends as well. This would lead to the necessity that every modifier must be a friend of its data structure. But who can guarantee, that no modifier is forgotten?
A solution is, that modification strategies are not implemented by ``external'' classes as iterators are. Instead, they are implemented by inheritance. If a sorted list is needed, it is a specialization of the general list. This sorted list would add a method, say insert(), which inserts a new element according to the modification strategy.
To make this possible, the presented list template must be changed. Because now, derived classes must have access to the head and tail node to implement these strategies. Consequently, _head and _tail should be protected.
The presented iterator implementation assumes, that the data structure is not changed during the use of an iterator. Consider the following example to illustrate this:
List<int> ilist;
int ix;
for (ix = 1; ix < 10; ix++)
ilist.append(ix);
ListIterator<int> iter(ilist);
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
printf("\n");
ilist.putInFront(0);
iter.rewind();
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
printf("\n");
This code fragment prints
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
instead of
1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
This is due to the fact, that our list iterator only stores pointers to the list structural elements. Thus, the start element _start is initially set to point to the location where the list's head node _head points to. This simply leads to two different pointers referencing the same location. Consequently, when changing one pointer as it is done by invoking putInFront() the other pointer is not affected.
For that reason, when rewinding the iterator after putInFront() the current element is set to the start element which was set at the time the iterator constructor was called. Now, the start element actually references the second element of the list.
T &operator ++() {
succ();
return _current->data();
}
What problems occur?
int remove(const T &data);to class template List. The method should delete the first occurrence of data in the list. The method should return 1 if it removed an element or 0 (zero) otherwise.
What functionality must data provide? Remember that it can be of any type, especially user defined classes!
MODULE Integer-List
DECLARE TYPE int_list_handle_t;
int_list_handle_t int_list_create();
BOOL int_list_append(int_list_handle_t this,
int data);
INTEGER int_list_getFirst(int_list_handle_t this);
INTEGER int_list_getNext(int_list_handle_t this);
BOOL int_list_isEmpty(int_list_handle_t this);
END Integer-List;
This representation introduces additional problems which are caused by not separating traversal from data structure. As you may recall, to iterate over the elements of the list, we have used a loop statement with the following condition:
WHILE data IS VALID DO
Data was initialized by a call to list_getFirst(). The integer list procedure int_list_getFirst() returns an integer, consequently, there is no such thing like an ``invalid integer'' which we could use for loop termination checking.
mul(k) div(k) abs()
The operation mul does not require any precondition. That's similar to add and sub. The postcondition is of course res = N*k. The next operation div requires k to be not 0 (zero). Consequently, we define the following precondition: k not equal 0. The last operation abs returns the value of N if N is positive or 0 or -N if N is negative. Again it does not matter what value N has when this operation is applied. Here is its postcondition:
class Complex {
attributes:
Real real,
imaginary
methods:
:=(Complex c) /* Set value to the one of c */
Real realPart()
Real imaginaryPart()
Complex +(Complex c)
Complex -(Complex c)
Complex /(Complex c)
Complex *(Complex c)
}
We choose the well-known operator symbols ``+'' for addition, ``-'' for subtraction, ``/'' for division and ``*'' for multiplication to implement the corresponding operations of the ADT Complex. Thus, objects of class Complex can be used like:
Complex c1, c2, c3 c3 := c1 + c2
You may notice, that we could write the addition statement as follows:
c3 := c1.+(c2)
You may want to replace the ``+'' with ``add'' to come to a representation which we have used so far. However, you should be able to understand that ``+'' is nothing more than a different name for ``add''.
class Rectangle inherits from Point {
attributes:
int _width, // Width of rectangle
_height // Height of rectangle
methods:
setWidth(int newWidth)
getWidth()
setHeight(int newHeight)
getHeight()
}
In this example, we define a rectangle by its upper left corner (coordinates as inherited from Point) and its dimension. Alternatively, we could have defined it by its upper left and lower right corner.
We add access methods for the rectangle's width and height.
class Sphere inherits from 3D-Point {
attributes:
int _radius;
methods:
setRadius(int newRadius)
getRadius()
}
This is similar to the circle class for 2D space. Now, 3D-Point is just a Point with an additional dimension:
class 3D-Point inherits from Point {
attributes:
int _z;
methods:
setZ(int newZ);
getZ();
}
Consequently, 3D-Point and Point are related with a is-a relationship.
However, these properties are uniquely identified by following the path from D up to A. Thus, D can change properties of A inherited by B by following the inheritance path through B. Similarly, D can change properties of A inheritied by C by following the inheritance path through C. Consequently, this naming conflict does not necessarily lead to an error, as long as the paths are designated.
void display(const DrawableObject obj);First note, that in C++ function or method parameters are passed by value. Consequently, obj would be a copy of the actual provided function call argument. This means, that DrawableObject must be a class from which objects can be created. This is not the case, if DrawableObject is an abstract class (as it is when print() is defined as pure method.)
If there exists a virtual method print() which is defined by class DrawableObject, then (as obj is only a copy of the actual argument) this method is invoked. It is not the method defined by the class of the actual argument (because it does no longer play any significant role!)
T &operator ++() {
succ();
return(_current ? _current->data() : (T) 0);
}
However, this does not function as we now assume something about
T. It must be possible to cast it to a kind of ,,NULL`` value.
During the iteration, remove() must compare the provided data item successively with those in the list. Consequently, there might exist a comparison like:
if (data == current->data()) {
// found the item
}
Here we use the equation operator ,,==`` to compare both data items. As these items can be of any type, they especially can be objects of user defined classes. The question is: How is ,,equality`` defined for those new types? Consequently, to allow remove() to work properly, the list should only be used for types which define the comparison operator (namely, ,,==`` and ,,!=``) properly. Otherwise, default comparisons are used, which might lead to strange results.
class CountedList : public List {
int _count; // The number of elements
...
public:
...
virtual void append(const T data) {
_count++; // Increment it and ...
List::append(data); // ... use list append
}
...
}
Not every method can be implemented this way. In some methods, one must check whether _count needs to be altered or not. However, the main idea is, that each list method is just expanded (or specialized) for the counted list.
This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -html_version 3.0 -split +0 -show_section_numbers -no_navigation -t Introduction to Object-Oriented Programming -antialias -toc_stars -local_icons -dir huge tutorial.tex.
The translation was initiated by P. Mueller on 9/4/1997